傅立葉級數(shù)函數(shù)用于查找電路的穩(wěn)態(tài)響應。有四種不同類型的對稱性可用于簡化評估傅里葉系數(shù)的過程。

對稱性的影響

偶函數(shù)對稱性

奇函數(shù)對稱性

半波對稱

四分之一波對稱

偶函數(shù)對稱

當且僅當

f （ t ）= f （ - t ）1.1

如果函數(shù)滿足Eq。 1.1，然后它被認為是因為只有偶數(shù)指數(shù)的多項式函數(shù)具有這種類型的行為。對于任何偶數(shù)周期函數(shù)，傅里葉系數(shù)的方程式簡化如下：

$$ a_ {v} = \ frac {2} {T} \ int_ {0 } ^ {T/2} f（t）dt。$$（1.2）

$$ a_ {k} = \ frac {4} {T} \ int_ {0} ^ {T/2所有 k （1.4）的f（t）\ cos k \ omega _ {0} tdt。$$（1.3）

$$ b_ {k} = 0 $$ ）

注意方程式1.4，如果函數(shù)是偶數(shù)，則所有 b 系數(shù)都為零。下面，圖1.1描繪了偶數(shù)周期函數(shù)。以下兩個衍生物完全遵循方程式。 1.2 - 1.4。通過每次推導，選擇$$ t_ {0} = -T/2 $$，然后我們將積分間隔從 - T /2分解為0和0到 T /2，或如下

$$ a_ {v} = \ frac {1} {T} \ int _ { - T/2} ^ { T/2} f（t）dt $$

$$ = \ frac {1} {T} \ int _ { - T/2} ^ {0} f（t）dt + \ int_ { 0} ^ {T/2} f（t）dt。$$（1.5）

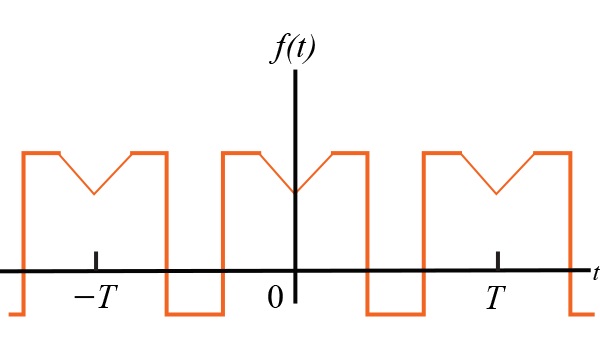
圖1.1偶數(shù)函數(shù)off（t）= f（-t）

現(xiàn)在，必須更改積分變量在方程式右邊的第一個積分中。 1.5。特別是，我們可以讓 t = - x 并觀察 f （ t ）= f （ - x ）= f （ x ），因為函數(shù)是偶數(shù)。當 t = - T /2和 dt x = T /2 = -dx 。因此

$$ \ int _ { - T/2} ^ {0} f（t）dt = \ int_ {T/2} ^ {0} f（x） （-dx）= \ int_ {0} ^ {T/2} f（x）dx。$$（1.6）

它確實表明從 - T /2到0與從0到 T /2的積分相同。因此，Eq。 1.5與Eq相同。 1.2。得出方程1.3可以完成如下：

$$ a_ {k} = \ frac {2} {T} \ int _ { - T/2} ^ {0} f（ t）\ cos k \ omega _ {0} tdt + \ frac {2} {T} \ int_ {0} ^ {T/2} \ cos k \ omega _ {0} tdt $$（1.7）

但是

$$ \ int _ { - T/2} ^ {0} f（t）\ cos k \ omega _ {0} tdt = \ int_ {T/2} ^ { 0} f（x）\ cos（-k \ omega _ {0} x）（ - dx）$$

$$ = - \ int_ {0} ^ {T/2} f（x ）\ cos k \ omega _ {0} xdx。$$（1.8）

同樣，如前所述，從 - T /2集成到0與從0到 T /2的積分相同。通過結合Eq。 1.7與Eq。 1.8，Eq。 1.3是生產的。在此之后，當 f （ t ）是偶數(shù)周期函數(shù)時，所有 b 系數(shù)都為零，因為積分來自 - T /2到0是從0到 T /2的積分的精確負數(shù)。因此，

$$ \ int _ { - T/2} ^ {0} f（t）\ sin k \ omega _ {0} tdt = \ int_ {T/2} ^ {0} f（x）\ sin（ -k \ omega _ {0} x）（ - dx）$$

$$ = - \ int_ {0} ^ {T/2} f（x）\ sin k \ omega _ {0 } xdx。$$（1.9）

現(xiàn)在，如果Eqs。 1.2和1.3用于查找傅里葉系數(shù)，積分區(qū)間必須介于0和 T /2之間。

奇函數(shù)對稱

如果

f （ t ）= - f （ t ）（1.10）

滿足公式的函數(shù)。 1.10被認為是奇數(shù)，因為只有奇數(shù)指數(shù)的多項式函數(shù)就是這樣的。傅里葉系數(shù)的表達式如下：

$$ a_ {v} = 0; $$（1.11）

$$ a_ {k} = 0，所有的$$ K表; （1.12）

$$ b_ {k} = \ frac {4} {T} \ int_ {0} ^ {T/2} f（t）\ sin k \ omega _ {0} dt 。$$（1.13）

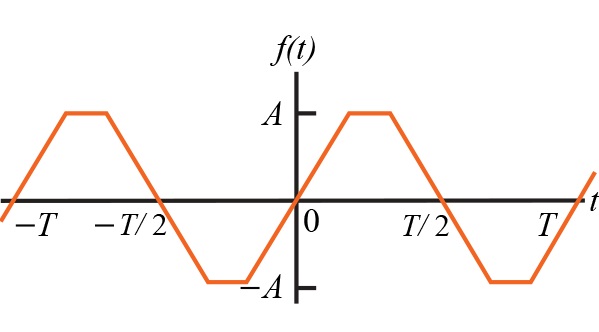
圖1.2

看著Eqs。 1.11 - 1.13，如果周期函數(shù)為奇數(shù)，則所有 a 系數(shù)均為零。上圖顯示了奇數(shù)周期函數(shù)。在方程式上使用相同的推導方法。 1.11 - 1.13，用于推導方程式。 1.2 - 1.4。

通過沿時間軸移動周期函數(shù)，可以拆除函數(shù)的均勻度（奇數(shù)）。從本質上講，這意味著明智地選擇 t = 0的位置可能會產生奇數(shù)或偶數(shù)對稱的函數(shù)。例如，圖1.3（a）中的三角函數(shù)不是偶數(shù)或奇數(shù)。然而，如圖1.3（b）所示，該函數(shù)可以是偶數(shù)，或者是奇數(shù)，如圖1.3（c）所示。

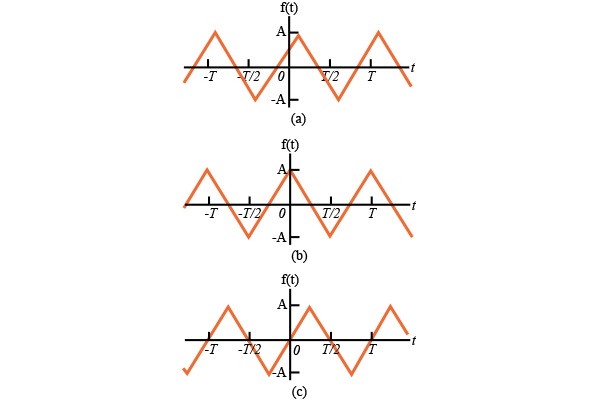
圖1.3

半波對稱

如果滿足以下約束，則稱該函數(shù)具有半波對稱性：

f （ t ）= - f （ t - T /2）（1.14）

公式1.14表示一個周期函數(shù)具有半波對稱性，如果它在被移動了一半的周期后被反轉，那就說與原始周期函數(shù)相同。例如，圖1.2和1.3中所示的周期函數(shù)具有半波對稱性，而圖1.4和1.5中的那些函數(shù)不具有這種對稱性。對于 t = 0，半波對稱性不作為函數(shù)存在。

如果給定函數(shù)確實具有半波對稱性，則 a

k 的偶數(shù)值，em> k 和 b k 被定義為零。類似地，由于具有這種對稱性的周期函數(shù)的平均值零， a v 也為零。傅里葉系數(shù)的表達式如下：

$$ a_ {v} = 0，$$（1.15）

$$ a_ {k} = 0，$$ k 偶數(shù)（1.16）

$$ a_ {k} = \ frac {4} {T} \ int_ {0} ^ {T/2 } f（t）\ cos k \ omega_ {0} tdt，$$ k odd（1.17）

$$ b_ {k} = 0，$$ for k even（1.18）

$$ b_ {k} = \ frac {4} {T} \ int_ {0} ^ {T/2} f（t）\ sin k \ omega_ {0} tdt，$$ k odd（1.19）

這些方程式來源于上一篇文章中的方程1.2 - 1.4，了解傅立葉系數(shù)。選擇從 - T /2到 T /2的積分間隔，然后將此范圍劃分為間隔 - T /2到0和0到 T /2。

$$ a_ {k} = \ frac {2} {T} \ int_ {t_ {0 }} {t_ {0} + T} f（t）\ cos k \ omega_ {0} tdt $$

$$ = \ frac {2} {T} \ int _ { - T/2} ^ {T/2} f（t）\ cos k \ omega_ {0} tdt $$

$$ = \ frac {2} {T} \ int _ { - T/2} ^ {0} f（t）\ cos k \ omega_ {0} tdt $$

$$ + \ frac {2} {T} \ int_ {0} ^ {T/2} f（t ）\ cos k \ omega_ {0} tdt $$（1.20）

從此處，右側第一個積分中的變量發(fā)生變化。

噸 = X - ?/2

然后

x = T /2，如果 t = 0

x = 0，如果 t = - T /2;

dt = dx

重寫第一個積分，

$$ \ int _ { - T/2} ^ {0} f（t）\ cos k \ omega_ {0} tdt = \ int_ {0} ^ {T/2} f（x - T/2）\ cos k \ omega_ {0}（x - T/2）dx $$（1.21）

考慮到

$$ \ cos k \ omega_ {0}（x - T/2）= \ cos（k \ omega_ {0} x - k \ pi）= \ cos k \ pi \ cos k \ omega_ {0} x $$

和b假設，

f （ x - T /2）= - f （ Ix ）

因此，Eq。 1.21現(xiàn)在可以寫成

$$ \ int _ { - T/2} ^ {0} f（t）\ cos k \ omega_ {0} tdt = \ int_ {0} ^ {T/2} [ - f（x）] \ cos k \ omega_ {0} tdt $$（1.22）

通過包括Eq。 1.22進入方程1.20，

$$ a_ {k} = \ frac {2} {T}（1 - \ cos k \ pi）\ int_ {0} ^ {T/2} f（t ）\ cos k \ omega_ {0} tdt $$（1.23）

但是，如果 k 為偶數(shù)，則$$ \ cos k \ pi $$等于1，如果 k 為奇數(shù)，則為-1。

總而言之，具有半波對稱零平均值的周期函數(shù)的傅里葉級數(shù)的表示僅包含奇數(shù)諧波。

四分之一波對稱

如果一個函數(shù)具有關于正和負半周期中點的半波對稱性和對稱性，則稱周期函數(shù)具有四分之一 - 波對稱。該功能如圖1.4所示;據(jù)說圖1.4（a）中的函數(shù)關于正半周期和負半周期的中點具有四分之一波對稱性。圖1.4（b）中的函數(shù)沒有這種對稱性，但它確實具有半波對稱性。

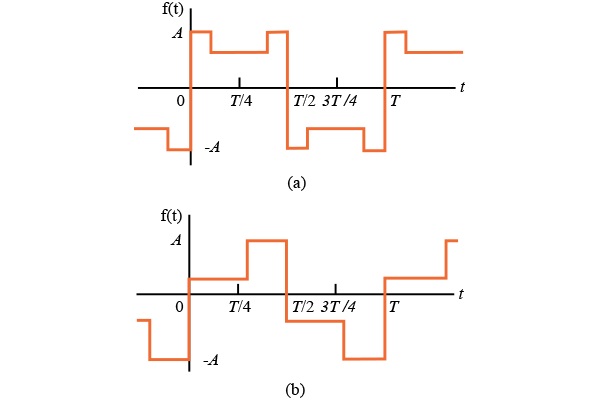
圖1.4

通過選擇 t = 0的位置，具有四分之一波對稱性的函數(shù)總是可以是偶數(shù)或奇數(shù)。例如，圖1.4（a）中的周期函數(shù)是奇數(shù)，可以通過沿著 t 向左或向右移動 T /4個單位變成偶數(shù)函數(shù) - 軸。但是，因為圖1.4（b）中的周期函數(shù)只具有半波對稱性，所以它不能是偶數(shù)或奇數(shù)。

如果要使周期函數(shù)均勻，那么

$$ a_ {v} = 0，$$由于半波對稱

$$ a_ {k} = 0，$$ for k 偶數(shù)，由于半波對稱性

$$ a_ {k} = \ frac {8} {T} \ int_ {0} ^ {T/4} f（t） \ cos k \ omega_ {0} tdt，$$ k 奇數(shù)

$$ b_ {k} = 0，所有 k 的$$ ，因為周期函數(shù)是偶數(shù)（1.24）

上面的Eqs。 1.24是周期函數(shù)對稱性的結果，除了它是偶數(shù)。如果四分之一波對稱性疊加在半波對稱上， a v 和 a k 因此， k 甚至可以被淘汰。看一下 a k 和 k odd，Eq的表達式。 1.19表明，當四分之一波對稱性與均勻度相結合時，積分范圍從0到 T /2縮短為0到 T /4。

如果四分之一波對稱周期函數(shù)為奇數(shù)，

$$ a_ {v} = 0，$$由于函數(shù)為奇數(shù)

$$ a_ {k} = 0，所有 k 的$$，由于函數(shù)為奇數(shù)

$$ b_ {k} = 0，$$ for k 甚至，由于半對稱性

$$ b_ {k} = \ frac {8} {T} \ int_ {0} ^ {T/4} f（ t）\ sin k \ omega_ {0} tdt，$$ k 奇數(shù)（1.25）

上面的1.25的Eq因此而來四分之一波對稱性和奇數(shù)。與均勻度相似，四分之一波對稱性允許從0到 T /2到0到 T /4的積分間隔縮短。

即將到來

截至目前，您應該更好地了解傅立葉系數(shù)和可能發(fā)生的不同類型的對稱性。這五種類型，偶數(shù)，奇數(shù)，半波，四分之一波半波甚至四分之一波半波都用于簡化傅立葉系數(shù)的計算。下面將介紹的一些主題將深入探討傅立葉級數(shù)的線性電路的穩(wěn)態(tài)響應，周期函數(shù)的平均功率計算，以及此類周期函數(shù)的均方根值。