引：

最近在搞一個音頻解碼器，將隨意錄制好的聲音按照不同的頻率分離出不同的音頻流，然后推到不同的音箱中，如果再考慮一下音場的諧性，那就是一個N.1聲道的解碼系統了。我只是想在女兒(或者兒子)出生之前為她做點事情，以便能最終做出個東西送給她(或者他)。

在實踐的過程中，遇到了傅里葉變換，作文以記之。最終我會導出一個很常用的變換-傅里葉變換

信號：

信號是一個很廣義的概念，它可以是一種波，也可以是一個陣列，它還可以是一個函數，它甚至是整個世界，總之只要能運載信息，它就可以被稱為信號 。我們可以去分析一個信號，以獲得信號本身更多的屬性，從而可以更好的獲得信息。比如，我們發現了諧波信號，我們就可以用波的理論去構造復雜的復合信號，典型就是頻分復用。

欲想理 解信號，我們首先要學會將其分解，將之分解成不同的元素，如果這些元素之間互不相關，我們就可以對其分而治之了，分而解之了。我們需要有一個信念，那就是所有的信號都是可分解的，我們必須明白這個復雜的世界其實是由很多次復雜的小世界疊加而成的，每一個次復雜的小世界都是由更簡單的次次復雜的小小世界疊加而成的，諸如此類，以此類推，最終的元素就是質子和電子(如果不想提夸克或者弦理論的話)。如果我們有了這個信念，我們就可以將一個信號分解成不同的信號的疊加。

比如一個物理概念，力，按照作用效果來說，它可以被分解在不同的兩個方向，如果這兩個方向互相垂直的話，那么一個方向的分力在另一個方向上沒有效果，我們說這兩個方向是正交的，當然，正交是一個數學概念。同樣的道理，一個函數，如果我們將它當成一個矢量的話，我們也可以將之分解，關鍵問題是我們基于什么去分解它，在《碼分多址(CDMA)的本質-正交之美》中，我們知道了正交多維矢量的概念，如果我們能找到一組正交的矢量，我們就可以將一個函數基于這組矢量進行分解。

尋找正交矢量：

對于信號，如果我們想用諧波來表示它的話，我們最好基于不同的頻率將之進行分解，那么接下來的問題就是尋找一個正交基，它可以表示不同的頻率的諧波。換句話說，我們希望用不同頻率的諧波的疊加來表示原始函數。我們也就是尋找一組函數I，使得下列正交條件成立：

由于簡諧波本身可以表示成三角函數，通過分析三角函數，我們發現下面的I函數系列滿足正交條件：

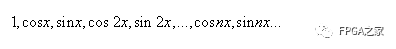
表示：

既然有了表示方法，接下來就是確定a，b等系數了，這些系數其實就是f(x)在各個相互正交的三角函數“坐標軸”上的分量，由于它們彼此都是正交的，我們能確定一個“坐標軸”上的分量不會在其它坐標軸上產生效果，因此它們的量是總的f(x)和該分量的乘積在區間a和b的積分，還記得公式

嗎？那是離散的情況，現在是它的連續情況！最終我們得到了系數b的表示法。所謂離散的情況和連續的情況區別僅在兩個符號：

離散的情況下，求和符號1直接相加了所有的項，而在連續的情況下，“一個項”需要由兩部分組成，即“積分表達式”和dx，每一個項都是這兩部分的乘積，并且各項的dx中的x是實數域的。

最終，我們得到了一個分解后的通用表示：

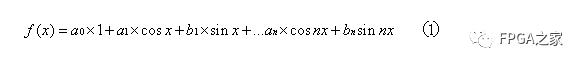
然后類比離散版的分量公式，求得了系數a和b，類比是次要的，重要的是：一個“坐標軸”上的分量不會在其它坐標軸上產生效果，因此它們的量是總的f(x)和該分量的乘積在區間a和b的積分 ：

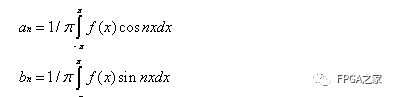
傅里葉變換：

其實已經說完了，以上的推導過程其實就是傅里葉變換，我們看得出，直到最后我才使用了積分公式，并且通篇沒有使用任何關于更深層的數學原理性的論述，我們發現，其實理解傅里葉變換并不需要太多數學，甚至都不需要微積分知識，你只需要直到一個道理：數學原理背后都有其物理模型，物理模型背后都有其現實解釋。

如果你確實將一個函數表示成了傅里葉級數，那么對于分析這個函數就太TM簡單了，以濾波為例，如果我們需要得到低頻信號，那么就可以將分量cosNx以后的全部丟掉，這樣，我們就可以得到任何頻率的信號了，N.1聲道的分頻自動就解決了。

傅里葉級數的現實解釋就是：任何一個信號都是多個周期信號疊加而成的。我們可以用我們學過的波的干涉原理來理解它，一個兩列簡諧波1,2疊加的波a，在任何時間點，波a的幅度都是波1和波2幅度的算術和！

后記：

碼分多址是將“碼”本身當成了正交分量，而傅里葉級數卻將頻率當成了正交分量，它們倆的本質是相同的，唯一不同的就是對其的物理解釋不同，如果我做了一個離散版本的傅里葉變換，過濾了高頻信號，和碼分多址的沃爾什編碼相比較一下，它們的公式最終是一模一樣了。

只要我們將一個信號按照一定的物理解釋進行分解，各種級數就都出來了，除了那些純數學的抽象解釋，泰勒級數遠比傅里葉級數更抽象，但是大多數教科書都是先講泰勒級數，即使這樣，泰勒級數也是有背后物理原理的，那就是任何一個大的變化都是由小的變化漸變而成的，哲學上的解釋就是量變和質變，我們有拐點和馬鞍面的概念！對一個函數的不斷求導其實就是挖掘它的變化層次，也就是最終有多少層的變化導致了最終函數曲線走向的變化。

本文沒有使用常規的方法且求解傅里葉級數系數，而是純粹從物理解釋方面上進行形象化的解釋和求解。傳統的求解方式也比較簡單就是在式子(1)兩邊同時乘以一個coskx和sinkx分別求解a和b，這是一種純數學的求解方式。

審核編輯 ：李倩