介紹
基于梯度下降訓(xùn)練神經(jīng)網(wǎng)絡(luò)時(shí),我們將冒網(wǎng)絡(luò)落入局部極小值的風(fēng)險(xiǎn),網(wǎng)絡(luò)在誤差平面上停止的位置并非整個(gè)平面的最低點(diǎn)。這是因?yàn)檎`差平面不是內(nèi)凸的,平面可能包含眾多不同于全局最小值的局部極小值。此外,盡管在訓(xùn)練數(shù)據(jù)上,網(wǎng)絡(luò)可能到達(dá)全局最小值,并收斂于所需點(diǎn),我們無(wú)法保證網(wǎng)絡(luò)所學(xué)的概括性有多好。這意味著它們傾向于過(guò)擬合訓(xùn)練數(shù)據(jù)。
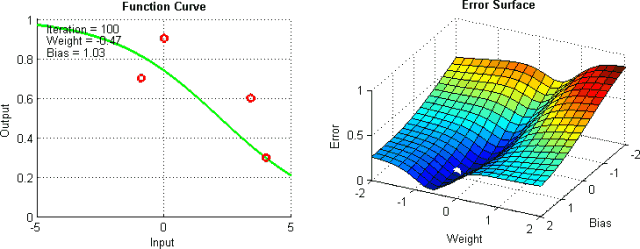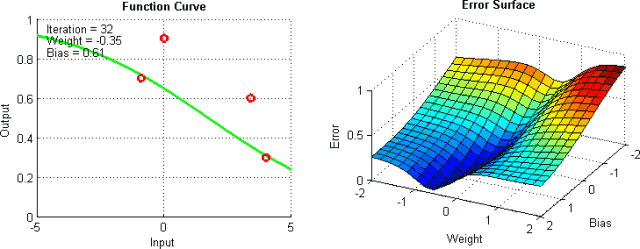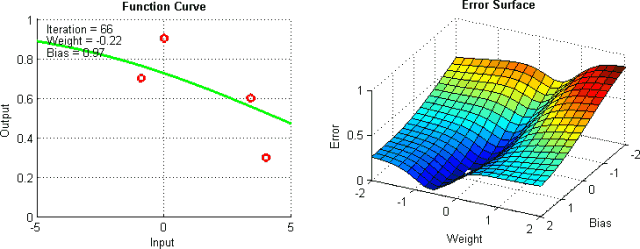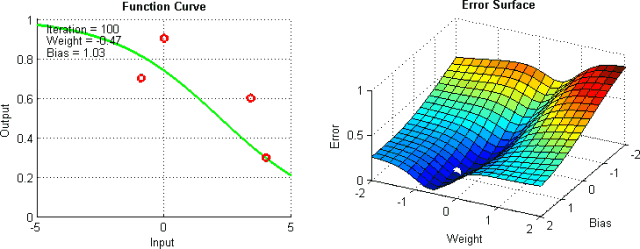
有一些手段有助于緩解這些問(wèn)題,不過(guò)并沒(méi)有絕對(duì)地預(yù)防這些問(wèn)題產(chǎn)生的方法。這是因?yàn)榫W(wǎng)絡(luò)的誤差平面一般很難穿越,而神經(jīng)網(wǎng)絡(luò)整體而言很難解釋。
隨機(jī)梯度下降與mini-batch隨機(jī)梯度下降
這些算法改編了標(biāo)準(zhǔn)梯度下降算法,在算法的每次迭代中使用訓(xùn)練數(shù)據(jù)的一個(gè)子集。SGD在每權(quán)重更新上使用一個(gè)樣本,mini-batch SGD使用預(yù)定義數(shù)目的樣本(通常遠(yuǎn)小于訓(xùn)練樣本的總數(shù))。這大大加速了訓(xùn)練,因?yàn)槲覀冊(cè)诿看蔚袥](méi)有使用整個(gè)數(shù)據(jù)集,它需要的計(jì)算量少得多。同時(shí),它也有望導(dǎo)向更好的表現(xiàn),因?yàn)榫W(wǎng)絡(luò)在訓(xùn)練中斷斷續(xù)續(xù)的移動(dòng)應(yīng)該能讓它更好地避開(kāi)局部極小值,而使用一小部分?jǐn)?shù)據(jù)集當(dāng)有助于預(yù)防過(guò)擬合。
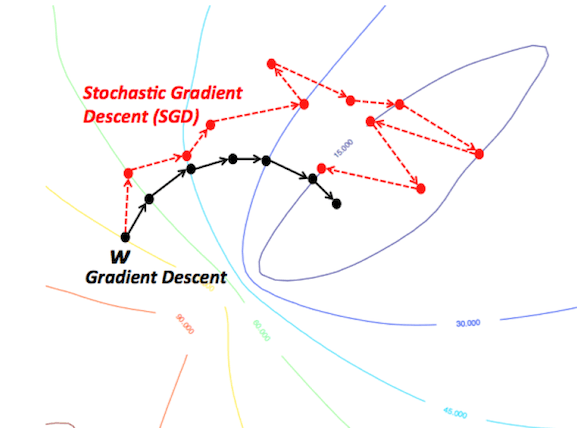
正則化
正則化基本上是一個(gè)懲罰模型復(fù)雜度的機(jī)制,它是通過(guò)在損失函數(shù)中加入一個(gè)表示模型復(fù)雜度的項(xiàng)做到這一點(diǎn)的。在神經(jīng)網(wǎng)絡(luò)的例子中,它懲罰較大的權(quán)重,較大的權(quán)重可能意味著神經(jīng)網(wǎng)絡(luò)過(guò)擬合了訓(xùn)練數(shù)據(jù)。
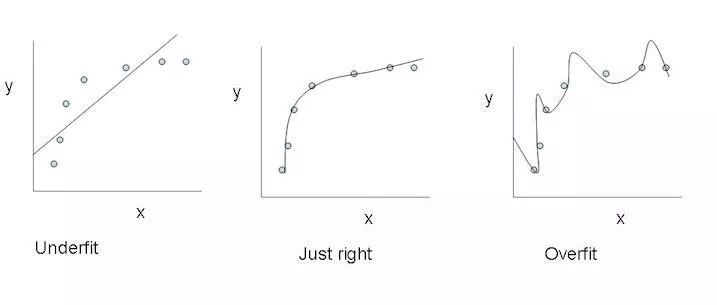
最左:欠擬合;最右:過(guò)擬合
若網(wǎng)絡(luò)的原損失函數(shù)記為L(zhǎng)(y, t),正則化常數(shù)記為λ,則應(yīng)用了L2正則化后,損失函數(shù)改寫(xiě)為如下形式:
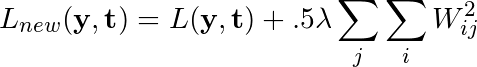
正則化在損失函數(shù)中加入了網(wǎng)絡(luò)的每個(gè)權(quán)重的平方和,以懲罰給任何一個(gè)連接分配了過(guò)多權(quán)重的模型,希望能降低過(guò)擬合程度。
動(dòng)量
簡(jiǎn)單來(lái)說(shuō),動(dòng)量在當(dāng)前權(quán)重更新上加上一小部分前次權(quán)重更新。這有助于預(yù)防模型陷入局部極小值,因?yàn)榧词巩?dāng)前梯度為0,之前梯度絕大多數(shù)情況下不為0,這樣模型就不那么容易陷入極小值。另外,使用動(dòng)量也使誤差平面上的移動(dòng)總體上更為平滑,而且移動(dòng)得更快。
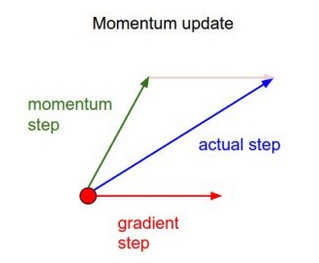
基于這一簡(jiǎn)單的動(dòng)量概念,我們可以重寫(xiě)權(quán)重更新等式至如下形式(α為動(dòng)量因子):
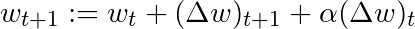
還有其他一些更高級(jí)的動(dòng)量形式,比如Nesterov方法。
學(xué)習(xí)率退火
我們可以不在整個(gè)訓(xùn)練過(guò)程中使用同一學(xué)習(xí)率,而是隨著時(shí)間的進(jìn)展降低學(xué)習(xí)率,也就是退火。
最常見(jiàn)的退火規(guī)劃基于1/t關(guān)系,如下圖所示,其中T和μ0為給定的超參數(shù),μ為當(dāng)前學(xué)習(xí)率:
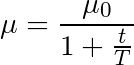
這經(jīng)常被稱為“搜索并收斂”(search-then-converge)退火規(guī)劃,因?yàn)橹钡絫達(dá)到T之前,網(wǎng)絡(luò)都處于“搜索”階段,學(xué)習(xí)率沒(méi)有下降很多,在此之后,學(xué)習(xí)率減慢,網(wǎng)絡(luò)進(jìn)入“收斂”階段。這和探索(exploitation)與利用(exploration)間的平衡多多少少有些關(guān)系。剛開(kāi)始我們優(yōu)先探索搜索空間,擴(kuò)展我們關(guān)于空間的整體知識(shí),隨著時(shí)間的推進(jìn),我們過(guò)渡到利用搜索空間中我們已經(jīng)找到的良好區(qū)域,收縮至特定的極小值。
結(jié)語(yǔ)
這些改進(jìn)標(biāo)準(zhǔn)梯度下降算法的方法都需要在模型中加入超參數(shù),因而會(huì)增加調(diào)整網(wǎng)絡(luò)所需的時(shí)間。最近提出的一些新算法,比如Adam、Adagrad、Adadelta,傾向于在每個(gè)參數(shù)的基礎(chǔ)上進(jìn)行優(yōu)化,而不是基于全局優(yōu)化,因此它們可以基于單獨(dú)情況精細(xì)地調(diào)整學(xué)習(xí)率。在實(shí)踐中,它們往往更快、更好。下圖同時(shí)演示了之前提到的梯度下降變體的工作過(guò)程。注意看,和簡(jiǎn)單的動(dòng)量或SGD相比,更復(fù)雜的變體收斂得更快。
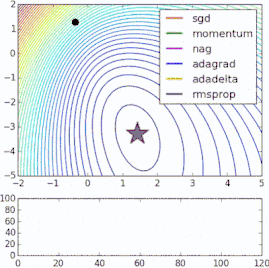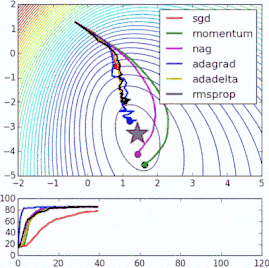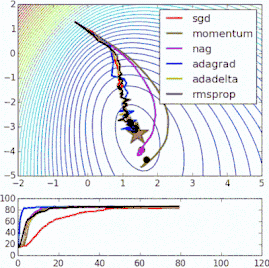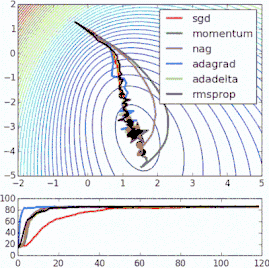
-
神經(jīng)網(wǎng)絡(luò)
+關(guān)注
關(guān)注
42文章
4811瀏覽量
103059 -
動(dòng)量
+關(guān)注
關(guān)注
0文章
6瀏覽量
7973 -
正則化
+關(guān)注
關(guān)注
0文章
17瀏覽量
8211
原文標(biāo)題:如何改進(jìn)梯度下降算法
文章出處:【微信號(hào):jqr_AI,微信公眾號(hào):論智】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
SGD的隨機(jī)項(xiàng)在其選擇最終的全局極小值點(diǎn)的關(guān)鍵性作用
如何對(duì)一波形所有極大(小)值點(diǎn)用三次樣條插值函數(shù)擬...
關(guān)于檢測(cè)的離散信號(hào)求極值問(wèn)題
分享一個(gè)自己寫(xiě)的機(jī)器學(xué)習(xí)線性回歸梯度下降算法
機(jī)器學(xué)習(xí)新手必學(xué)的三種優(yōu)化算法(牛頓法、梯度下降法、最速下降法)
改進(jìn)的BP網(wǎng)絡(luò)算法在圖像識(shí)別中的應(yīng)用

機(jī)器學(xué)習(xí):隨機(jī)梯度下降和批量梯度下降算法介紹
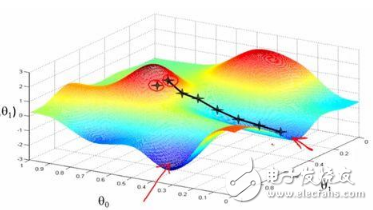
梯度下降算法及其變種:批量梯度下降,小批量梯度下降和隨機(jī)梯度下降
講解隨機(jī)梯度下降、類別數(shù)據(jù)編碼、Vowpal Wabbit機(jī)器學(xué)習(xí)庫(kù)
簡(jiǎn)單的梯度下降算法,你真的懂了嗎?
如何使用區(qū)域相似度實(shí)現(xiàn)局部擬合活動(dòng)輪廓模型
基于雙曲網(wǎng)絡(luò)空間嵌入與極小值聚類的社區(qū)劃分算法

基于局部熵擬合與全局信息的改進(jìn)活動(dòng)輪廓模型
JPEG LS算法局部梯度值計(jì)算原理





 梯度下降兩大痛點(diǎn):陷入局部極小值和過(guò)擬合
梯度下降兩大痛點(diǎn):陷入局部極小值和過(guò)擬合










評(píng)論