目前,還沒有人能夠真正理解深度網(wǎng)絡在目標分類任務方面的運行方式和原理。主要原因是對深度網(wǎng)絡在分類任務中所做的“工作”還沒有一個很好的衡量標準,一篇最近發(fā)表的關于“通用感知流形”理論的論文試圖解決這個問題。
這篇論文于7月5日發(fā)表在《Phisical Review X》上,題為《Classification and Geometry of General Perceptual Manifolds》。論文作者為哈佛大學工程和應用科學系的SueYeon Chung, 賓夕法尼亞大學工程與應用科學系的Daniel D. Lee以及哈佛大學大腦科學中心的Haim Sompolinsky。
用統(tǒng)計力學理解機器學習,分析分層網(wǎng)絡的表示
文章提出,當神經(jīng)元群對與相同感知目標的不同物理特征(如方向、姿勢、規(guī)模、位置和強度等)相關的感覺信號集合做出反應時,就會出現(xiàn)感知流形(Perceptual manifold)。對目標的識別和區(qū)分需要以對流形內(nèi)部變化不敏感的方式對流形進行分類。神經(jīng)元系統(tǒng)對不變目標的分類和識別是大腦理論和機器學習中的基本問題。
文章研究讀出網(wǎng)絡(readout network)從其流形表示中對對象進行分類的能力,開發(fā)了一種統(tǒng)計力學理論,用于對任意幾何形狀的流形進行線性分類,并表明該理論與圓錐分解在數(shù)學上顯著相關。文中表明,位于流形上的特殊錨點可以定義半徑和維度的新幾何學量度,這可以解釋各種幾何形狀的流形的分類能力。
這個通用理論已經(jīng)在許多有代表性的流形上得到證明,包括典型的嚴格凸流形的l2橢圓體流形,代表具有有限樣本的多面體的l1球流形,以及代表由于調(diào)節(jié)連續(xù)自由度而產(chǎn)生的非凸連續(xù)結構的環(huán)狀流形。同時我們也闡明了標注稀疏性對一般流形分類能力的影響,表明了標注稀疏與流形半徑之間存在廣泛的比例關系。文章使用新開發(fā)的算法計算多種二分法的最大邊際解,通過數(shù)值模擬證實了理論預測。此文提出的理論及其擴展提供了一個強大而豐富的框架,可用于將線性分類的統(tǒng)計力學應用于由感知神經(jīng)元響應產(chǎn)生的數(shù)據(jù)以及針對目標識別任務訓練的人工深度網(wǎng)絡中。
我們的大腦能夠準確地對我們看到的物體進行分類,就算這些不同的物體的屬性參數(shù)(比如亮度、形態(tài)和背景特征)彼此間存在巨大差異,對大腦而言也往往不成問題。機器學習的最新進展已經(jīng)產(chǎn)生了與我們的大腦具有相似能力的神經(jīng)網(wǎng)絡。然而,對生物和人工智能系統(tǒng)為何能達到如此高的識別準確性,研究人員對此問題在數(shù)學上還不夠理解。本文展示了如何使用統(tǒng)計力學理論來解釋這個問題的基本原理,這些原理是神經(jīng)回路面對巨大的物理上可變性時,仍能具備識別和區(qū)分目標的能力的基礎。
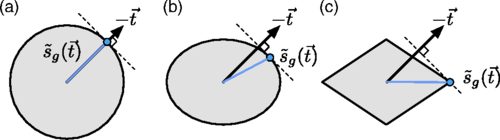
本文將特定對象的神經(jīng)表示中的可變性經(jīng)幾何建模為流形。在網(wǎng)絡的特定階段能夠被成功分類的流形數(shù)量的增長與神經(jīng)表示的維度成正比,但具體比例取決于流形的形狀。我們的理論可以分析在網(wǎng)絡中變化和傳導的流形表示的結構,最終將其成功分類。
本文提出的理論利用圖形學量度來描述神經(jīng)流形的形狀,這些量度能夠預測何時可以分離篩選出隨機標記的流形集。這些測量導致了具有任意幾何形狀的流形的數(shù)量,并且可以有效地計算;我們用它們來分析神經(jīng)反應的原型流形模型。
本文提供了一個新的理論框架來理解和分析由分層神經(jīng)網(wǎng)絡形成的表示,可能會促進關于感知系統(tǒng)如何有效地編碼和處理感官信息的新見解。
長期以來,感知學習的統(tǒng)計力學理論為理解單層神經(jīng)架構及其內(nèi)核擴展的性能和基本局限性打下了基礎。然而,以前的理論僅考慮了不存在圖形架構的、有限數(shù)量的隨機點,并且無法解釋由于物理參數(shù)變化引起的可變性增加,而呈現(xiàn)為不同流形的大規(guī)模、可能是無限數(shù)量的輸入時,線性分類器的性能下降問題。本研究中提出的統(tǒng)計力學理論,可以解釋一般流形的線性分類的能力和局限性,并用于闡明層次感覺系統(tǒng)中神經(jīng)表征的變化。我們相信這一理論的應用及其推論的擴展將為人們?nèi)绾斡行У鼐幋a和處理感官信息的感知系統(tǒng)提供新的見解。
識別流形的通用理論:哪種網(wǎng)絡條件可以識別出流形
此文在Reddit論壇的機器學習板塊引發(fā)了一些很有意思的討論。不過,Reddit上有小伙伴表示論文的專業(yè)用語讓他看起來“就像個5歲小孩,求大神解釋”。下面有好幾位熱心觀眾用比較通俗的用語和示例對此文給出了自己的解釋。
比方說,你平生第一次見到一只貓,即使這只貓離你很遠,又蜷曲著身子,但從它的體型形狀上判斷,仍然能夠知道這是只貓。這篇論文提出的方法,就是要教會機器也掌握類似的識別方式,從目標的幾何形狀上來猜測,這是什么東西。也就是說,給計算機看一堆圖形,然后讓它猜測剩余部分是什么樣子的,而不用從每個角度來觀察目標。
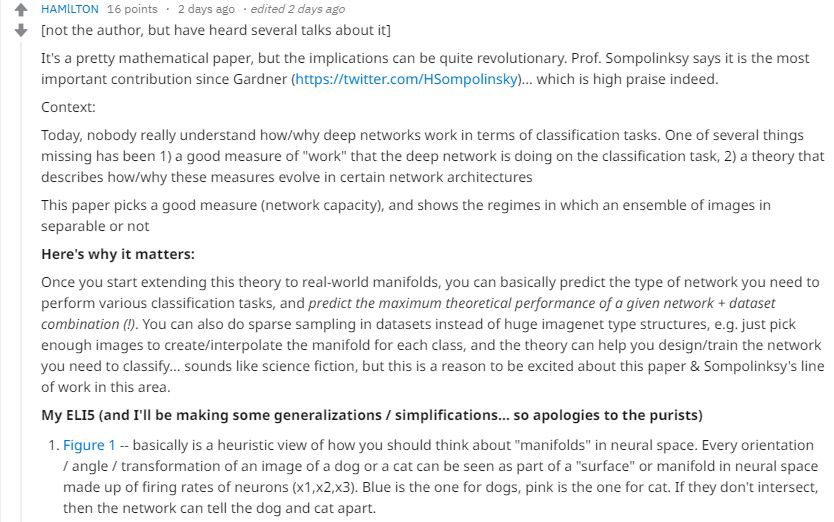
其中一位ID為“Hanmilton”的壇友給出了比較系統(tǒng)和詳實的回復(如上圖)。他首先聲明,自己并不是這篇論文的作者,但曾有幸聽過作者之一的學術報告。他認為,這是一篇偏數(shù)學的論文,但其結論是頗具“革新性”的,接著在留言中從研究背景、重要性、應用意義上對文章進行了概述和分析。新智元對相關內(nèi)容做了編譯,一起來看看:
他表示,論文中的圖1(下圖)基本上提供了關于神經(jīng)空間中“流形”概念的啟發(fā)性觀點。在神經(jīng)空間中,我們對一只貓或狗的每個觀察的方向/角度/位置變化都可以視作一個由神經(jīng)元放電頻率構成的平面或“流形”。圖中藍色對應為狗,粉色對應為貓。如果這兩個區(qū)域沒有交集,神經(jīng)網(wǎng)絡就能夠分辨出貓和狗。
他認為,對目標的“神經(jīng)流形”表示是深度網(wǎng)絡理解目標和大腦識別/看見目標的框架。
2.論文其余部分是建立一個通用理論,告訴你哪種網(wǎng)絡條件可以識別出流形,哪種則不能識別。比如,你什么時候能分辨出貓和狗,什么時候分不出來。論文中花了不少的篇幅來構建關于流形如何存在于子空間內(nèi)的理論架構,如何用數(shù)學來描述(如下圖)。
3.文中用了一些實例來證明這個理論。其實可以使用貓和狗的,但作者使用了更為通用的形狀:球形、橢圓體和環(huán)狀。
4. 文章表明,該理論可以根據(jù)流形的特點來預測哪些流形可以識別,哪些識別不出。可以看到,在給定的維度上(比如D=20),隨著半徑的擴大,可識別度會下降,也就是說,這能夠顯示出在給定數(shù)據(jù)下所構建的網(wǎng)絡的極限。
-
神經(jīng)網(wǎng)絡
+關注
關注
42文章
4811瀏覽量
103019 -
機器學習
+關注
關注
66文章
8496瀏覽量
134218
原文標題:【深度學習再突破】讓計算機一眼認出“貓”:哈佛提出新高維數(shù)據(jù)分析法
文章出處:【微信號:AI_era,微信公眾號:新智元】歡迎添加關注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
人工神經(jīng)網(wǎng)絡原理及下載
【PYNQ-Z2試用體驗】神經(jīng)網(wǎng)絡基礎知識
【案例分享】ART神經(jīng)網(wǎng)絡與SOM神經(jīng)網(wǎng)絡
基于BP神經(jīng)網(wǎng)絡的PID控制
卷積神經(jīng)網(wǎng)絡模型發(fā)展及應用
卷積神經(jīng)網(wǎng)絡簡介:什么是機器學習?
模糊神經(jīng)網(wǎng)絡的優(yōu)缺點分析
神經(jīng)網(wǎng)絡理論到實踐(2):理解并實現(xiàn)反向傳播及驗證神經(jīng)網(wǎng)絡是否正確
用Python從頭實現(xiàn)一個神經(jīng)網(wǎng)絡來理解神經(jīng)網(wǎng)絡的原理1
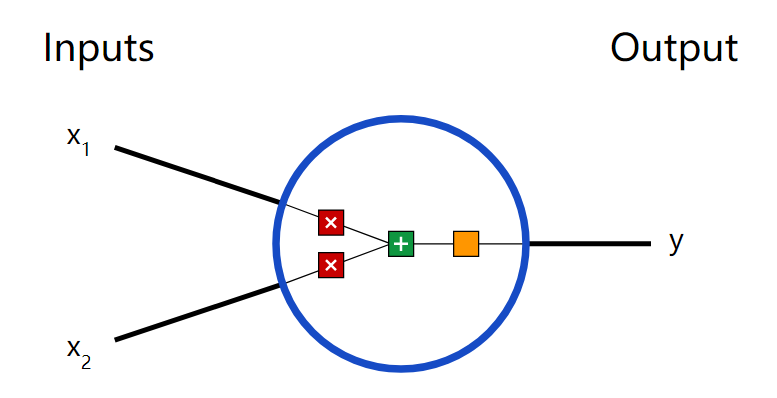
用Python從頭實現(xiàn)一個神經(jīng)網(wǎng)絡來理解神經(jīng)網(wǎng)絡的原理2
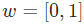
用Python從頭實現(xiàn)一個神經(jīng)網(wǎng)絡來理解神經(jīng)網(wǎng)絡的原理3

用Python從頭實現(xiàn)一個神經(jīng)網(wǎng)絡來理解神經(jīng)網(wǎng)絡的原理4

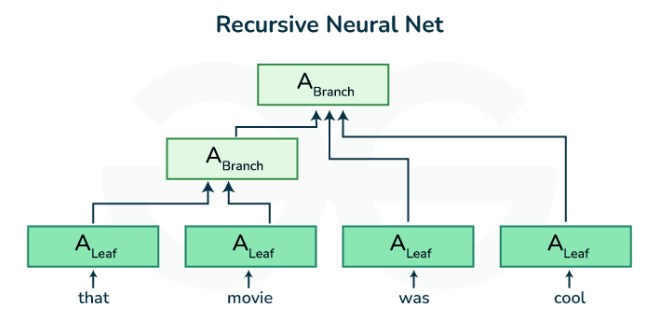
遞歸神經(jīng)網(wǎng)絡和循環(huán)神經(jīng)網(wǎng)絡的模型結構





 一個新的理論框架來理解和分析由分層神經(jīng)網(wǎng)絡形成的表示
一個新的理論框架來理解和分析由分層神經(jīng)網(wǎng)絡形成的表示










評論