邊緣檢測的理解可以結合前面的內核，說到內核在圖像中的應用還真是多，到現在為止學的對圖像的操作都是核的操作，下面還有更神奇的！

　　想把邊緣檢測出來，從圖像像素的角度去想，那就是像素值差別很大，比如X1=20和X2=200，這兩個像素差值180，在圖像的顯示就非常明顯，這樣圖像的邊緣不就體現出來了？但是問題來了，一幅圖像給你，如果一個像素一個像素對比，

　　邊緣檢測原理及步驟

　　在之前的博文中，作者從一維函數的躍變檢測開始，循序漸進的對二維圖像邊緣檢測的基本原理進行了通俗化的描述。結論是：實現圖像的邊緣檢測，就是要用離散化梯度逼近函數根據二維灰度矩陣梯度向量來尋找圖像灰度矩陣的灰度躍變位置，然后在圖像中將這些位置的點連起來就構成了所謂的圖像邊緣（圖像邊緣在這里是一個統稱，包括了二維圖像上的邊緣、角點、紋理等基元圖）。

　　在實際情況中理想的灰度階躍及其線條邊緣圖像是很少見到的，同時大多數的傳感器件具有低頻濾波特性，這樣會使得階躍邊緣變為斜坡性邊緣，看起來其中的強度變化不是瞬間的，而是跨越了一定的距離。這就使得在邊緣檢測中首先要進行的工作是濾波。

　　1）濾波：邊緣檢測的算法主要是基于圖像強度的一階和二階導數，但導數通常對噪聲很敏感，因此必須采用濾波器來改善與噪聲有關的邊緣檢測器的性能。常見的濾波方法主要有高斯濾波，即采用離散化的高斯函數產生一組歸一化的高斯核（具體見“高斯濾波原理及其編程離散化實現方法”一文），然后基于高斯核函數對圖像灰度矩陣的每一點進行加權求和（具體程序實現見下文）。

　　2）增強：增強邊緣的基礎是確定圖像各點鄰域強度的變化值。增強算法可以將圖像灰度點鄰域強度值有顯著變化的點凸顯出來。在具體編程實現時，可通過計算梯度幅值來確定。

　　3）檢測：經過增強的圖像，往往鄰域中有很多點的梯度值比較大，而在特定的應用中，這些點并不是我們要找的邊緣點，所以應該采用某種方法來對這些點進行取舍。實際工程中，常用的方法是通過閾值化方法來檢測。

　　邊緣檢測算法

　　1、Sobel邊緣檢測算法為例。

　　Sobel卷積核模板為：

　　偏導公式為：

　　2、Robert算子檢測邊緣：

　　x和y方向的算子

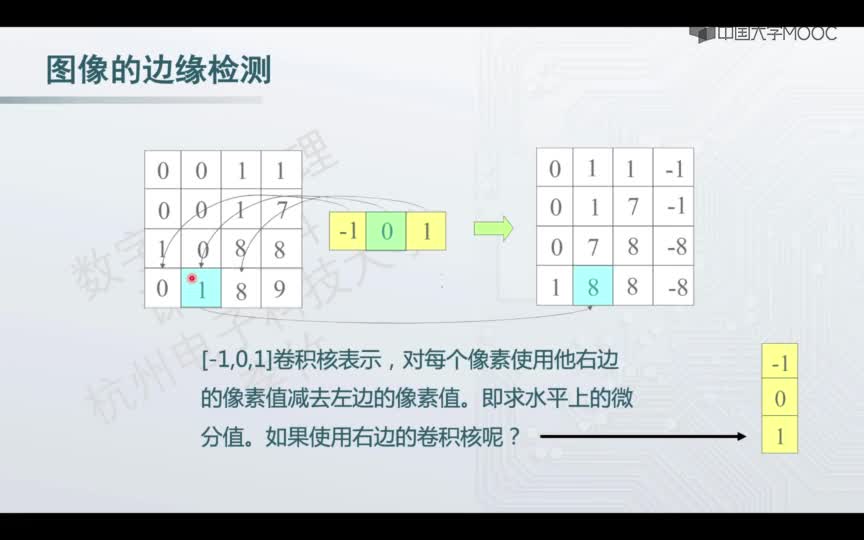
　　觀察上訴的算子，可以發現和我們剛開始設想的一個一個比較差不多，比如本來比如X1=20和X2=40，這兩個像素差值20，但是20體現不出來，所以用1，-1來增大這種差值，這其實解決了我們上訴遇到的第一點問題了，但是后面的兩點依然沒有解決。

　　具體的例子我們可以用opencv自帶的API，addwight進行試驗，把核改一下就行了。。。

　　Roberts算子檢測方法對具有陡峭的低噪聲的圖像處理效果較好，但是利用roberts算子提取邊緣的結果是邊緣比較粗，因此邊緣的定位不是很準確。

　　X和Y方向

　　對X\Y兩個方向的梯度進行合并

　　3、 Laplacian算子檢測邊緣：

　　拉普拉斯算子

　　拉普拉斯邊緣檢測是通過二階倒數，從上面的一階倒數的理解就不難發現二階倒數是怎么進行的了。

　　二階倒數比一階倒數的好處是在與受到周圍的干擾小，其不具有方向性，操作容易，且對于很多方向的圖像處理好。

　　Laplacian算子法對噪聲比較敏感，所以很少用該算子檢測邊緣，而是用來判斷邊緣像素視為與圖像的明區還是暗區。

　　4、Scharr算子檢測邊緣：

　　這個濾波是Sobel的升級版，原理是一樣的，就是實現的近似代替不一樣，說白了就事核改進了。。。

　　5、.Canny算子檢測邊緣：

　　這是比較新的算法，運用的也是最廣泛的。這個算法是在Sobel算法的基礎上改進的，和Scharr不一樣！

　　Canny的步驟是：1.給一張圖片，先進行濾波消除干擾，濾波前面博客已經說明。

　　2.計算梯度（進行Sobel算子計算）。

　　3.非極大值抑制。

　　4.滯后閾值。

　　下面一屆具體介紹-》》》》

　　在opencv2.0的時候，直接調用API就幫你完成全部的工作，包含上面的四部。

　　現在opencv3.0濾波得自己操作，API完成了后三步操作。

　　這里在Sobel運行之后的基礎上對圖像的邊緣進行了優化，哪些是優秀的，哪些是差的，在這里會處理。

　　---細談邊緣檢測---

　　上面講到Canny的非極大值抑制和滯后閾值，其中這兩點是這個算法的核心！

　　非極大值抑制：

　　從字面上的理解就是從一群數據中找到真正的極大值，對于不是極大值的省略或者抑制顯示。

　　我們來想一下，Sobel算子計算的值就是邊緣的值嗎？1.算子是固定的，那就有很大的幾率會計算到不是邊緣的數據。

　　2.計算的結果不會省略不好的點，也不會去加強好的點，所以顯示就不明顯。

　　我們的目的就是改進上面兩個點，對于第一個點，我們得比較那些計算的點進行比較，把不好點舍去---》》》

　　以前在神經網絡那篇博文里提到過“梯度”的概念，就是數據下降或者上升最快的方向，簡單的說就是求導切線的方向！

　　試想一下我們在這個方向上找最大和最小值是最快最準確的，這個具體原因神經網絡那篇博文說過了，可以去看看。

　　通過計算我們得到了θ的值在［-π/2，+π/2］區間，然后我們就可以比較在這個方向上的G和左右G1、G2的大小，當G》G1、G2的時候，那就說明這個G就是局部極大值，從而保留下來：

　　例如：G0的θ是45度，那么在它的梯度方向來對比它是不是最大值，如果是的話那就說明它是局部極大值-》判斷G0和（G3、G6）的大小關系！G0 = G0》G3&&G0》G6？ G0:0;

　　上面的方法是第一代非極大值抑制算法，缺點是當 θ！=0、45、90、180 時，那么旁邊的八個值就不在θ的梯度上，就沒辦法去做比較了，這時候出現第二代算法---》》》

　　插值法運用在非最大值抑制算法中：

　　插值法：就是y=kx+b的插值公式，比如：X1和X2中間想插一點X，X = X1 + k（X2-X1）或者X= k*X1 +（1-k）X2 當然插值法還有其它形式，不過兩點的線性插值比較簡單的。這里使用第二者！

　　上面的圖形是當 |Gy|》|Gx| && Gx*Gy》0 的情況。前者保障靠近y軸，后者保證θ》0.

　　注釋：在有的文章上看的和我說的相反，按照數學知識應該是這樣的啊，具體原因我也不知道了。

　　令 k = |Gy/Gx|

　　G23 = k*G2 + （1-k）*G3;

　　G67 = k*G6 + （1-k）*G7;

　　G0 = G0》G23 && G0》G67 ？ G0:0;或者這里可以突出重點給定G0的值G0 = G0》G23 && G0》G67 ？ 200:0;

　　opencv的源碼就是使用這種方法的，大家可以參考源碼：

　　1 void NonMaxSuppress（int*pMag，int* pGradX，int*pGradY，SIZE sz，LPBYTE pNSRst）

　　2 {

　　3 LONG x，y;

　　4 int nPos;

　　5 // the component of the gradient

　　6 int gx，gy;

　　7 // the temp varialbe

　　8 int g1，g2，g3，g4;

　　9 double weight;

　　10 double dTemp，dTemp1，dTemp2;

　　11 //設置圖像邊緣為不可能的分界點

　　12 for（x=0;x《sz.cx;x++）

　　13 {

　　14 pNSRst［x］ = 0;

　　15 pNSRst［（sz.cy-1）*sz.cx+x］ = 0;

　　16

　　17 }

　　18 for（y=0;y《sz.cy;y++）

　　19 {

　　20 pNSRst［y*sz.cx］ = 0;

　　21 pNSRst［y*sz.cx + sz.cx-1］ = 0;

　　22 }

　　23

　　24 for （y=1;y《sz.cy-1;y++）

　　25 {

　　26 for （x=1;x《sz.cx-1;x++）

　　27 {

　　28 nPos=y*sz.cx+x;

　　29 // if pMag［nPos］==0， then nPos is not the edge point

　　30 if （pMag［nPos］==0）

　　31 {

　　32 pNSRst［nPos］=0;

　　33 }

　　34 else

　　35 {

　　36 // the gradient of current point

　　37 dTemp=pMag［nPos］;

　　38 // x，y 方向導數

　　39 gx=pGradX［nPos］;

　　40 gy=pGradY［nPos］;

　　41 //如果方向導數y分量比x分量大，說明導數方向趨向于y分量

　　42 if （abs（gy）》abs（gx））

　　43 {

　　44 // calculate the factor of interplation

　　45 weight=fabs（gx）/fabs（gy）;

　　46 g2 = pMag［nPos-sz.cx］; // 上一行

　　47 g4 = pMag［nPos+sz.cx］; // 下一行

　　48 //如果x，y兩個方向導數的符號相同

　　49 //C 為當前像素，與g1-g3 的位置關系為：

　　50 //g1 g2

　　51 // C

　　52 // g4 g3

　　53 if（gx*gy》0）

　　54 {

　　55 g1 = pMag［nPos-sz.cx-1］;

　　56 g3 = pMag［nPos+sz.cx+1］;

　　57 }

　　58 //如果x，y兩個方向的方向導數方向相反

　　59 //C是當前像素，與g1-g3的關系為：

　　60 // g2 g1

　　61 // C

　　62 // g3 g4

　　63 else

　　64 {

　　65 g1 = pMag［nPos-sz.cx+1］;

　　66 g3 = pMag［nPos+sz.cx-1］;

　　67 }

　　68 }

　　69 else

　　70 {

　　71 //插值比例

　　72 weight = fabs（gy）/fabs（gx）;

　　73 g2 = pMag［nPos+1］; //后一列

　　74 g4 = pMag［nPos-1］; // 前一列

　　75 //如果x，y兩個方向的方向導數符號相同

　　76 //當前像素C與 g1-g4的關系為

　　77 // g3

　　78 // g4 C g2

　　79 // g1

　　80 if（gx * gy 》 0）

　　81 {

　　82 g1 = pMag［nPos+sz.cx+1］;

　　83 g3 = pMag［nPos-sz.cx-1］;

　　84 }

　　85

　　86 //如果x，y兩個方向導數的方向相反

　　87 // C與g1-g4的關系為

　　88 // g1

　　89 // g4 C g2

　　90 // g3

　　91 else

　　92 {

　　93 g1 = pMag［nPos-sz.cx+1］;

　　94 g3 = pMag［nPos+sz.cx-1］;

　　95 }

　　96 }

　　97 //--線性插值等價于dTemp1 = g1 + weight*（g2-g1）--//

　　98 dTemp1 = weight*g1 + （1-weight）*g2;

　　99 dTemp2 = weight*g3 + （1-weight）*g4;

　　100 //當前像素的梯度是局部的最大值

　　101 //該點可能是邊界點

　　102 if（dTemp》=dTemp1 && dTemp》=dTemp2）

　　103 {

　　104 pNSRst［nPos］ = 128;

　　105 }

　　106 else

　　107 {

　　108 //不可能是邊界點

　　109 pNSRst［nPos］ = 0;

　　110 }

　　111 }

　　112 }

　　113 }

　　114 }

　　在論文中海油一個改進的插值，用二次插值代替一次插值，學過數值分析的都知道，一次插值在直線很好，但是在曲線不好，當然二次插值也不能消除很多誤差，當然海油牛頓插值等等。

　　這是當Gx和Gy同號的情況，另一種情況自己想一下就行了。

　　二次插值相比較一次插值的優點是：不用考慮哪個哪個具體的角度。其實很多人都提到了0、45、90、180的角度劃分，我這里沒有提到，原理是一樣的，我感覺直接做就好了，沒必要再去弄個中間變量過度一下，可能為了理解吧。

　　滯后閾值：

　　1. T1， T2為閾值，凡是高于T2的都保留，凡是小于T1都丟棄。

　　2.如果介于T1和T2之間的話，判斷是否連接T2，如果沒連接T2那就刪除。

　　3.T1和T2比例最好1:2/1:3

　　這里說明一下第二點：

　　A.我們的目的是找到最大邊緣變化。

　　B.并且保證邊緣顯示效果很好。

　　對于A來說，我們非最大值抑制已經找到部分最大值，現在用T2再進行一遍，已經很好的達到我們A目的了。

　　對于B來說，用T1去濾去可能不是最大值的點，現在用第二點來加強顯示，在T2附近的保留，不在的都刪除（意思就是在最小值附近）。

　　看下面這個例子，T1=2，T2=9 用核3X3去找T2附近的值，那就表示只有6個值可以保留，其他值都將被刪除。

　　第一步：整個圖像去找T》T2和T《T1的值，刪除或者保留，并且標記記錄。

　　第二步：在上一步記錄的最大值附近尋找存在的值，直接刪除或者保留。