在圖像測量過程以及機(jī)器視覺應(yīng)用中,為確定空間物體表面某點(diǎn)的三維幾何位置與其在圖像中對應(yīng)點(diǎn)之間的相互關(guān)系,必須建立相機(jī)成像的幾何模型,這些幾何模型參數(shù)就是相機(jī)參數(shù)。在大多數(shù)條件下這些參數(shù)(內(nèi)參、外參、畸變參數(shù))必須通過實(shí)驗(yàn)與計(jì)算才能得到,這個求解參數(shù)的過程就稱之為相機(jī)標(biāo)定(或攝像機(jī)標(biāo)定)。無論是在圖像測量或者機(jī)器視覺應(yīng)用中,相機(jī)參數(shù)的標(biāo)定都是非常關(guān)鍵的環(huán)節(jié),其標(biāo)定結(jié)果的精度及算法的穩(wěn)定性直接影響相機(jī)工作產(chǎn)生結(jié)果的準(zhǔn)確性。因此,做好相機(jī)標(biāo)定是做好后續(xù)工作的前提,提高標(biāo)定精度是科研工作的重點(diǎn)所在。
標(biāo)定的目的主要為解決兩個問題:
a、確定世界坐標(biāo)系下三維空間點(diǎn)與像素平面像素點(diǎn)間的轉(zhuǎn)換關(guān)系(內(nèi)外參);
b、確定相機(jī)成像過程中的畸變系,用于圖像矯正。
針孔相機(jī)模型
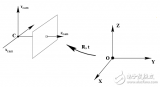
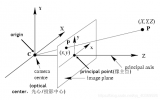
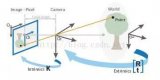
相機(jī)將三維世界中的坐標(biāo)點(diǎn)(單位:米)映射到二維圖像平面(單位:像素)的過程能夠用一個幾何模型來描述,其中最簡單的稱為針孔相機(jī)模型 (pinhole camera model),其框架如下圖所示:
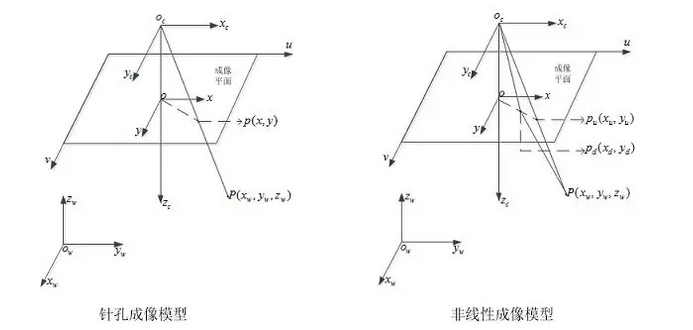
其中,涉及到相機(jī)標(biāo)定涉及到了四大坐標(biāo)系,分別為:
像素坐標(biāo)系(u,v):為了描述物體成像后的像點(diǎn)在數(shù)字圖像上(相片)的坐標(biāo)而引入,是我們真正從相機(jī)內(nèi)讀取到的信息所在的坐標(biāo)系。單位為個(像素?cái)?shù)目)。
成像平面坐標(biāo)系(x,y):為了描述成像過程中物體從相機(jī)坐標(biāo)系到圖像坐標(biāo)系的投影透射關(guān)系而引入,方便進(jìn)一步得到像素坐標(biāo)系下的坐標(biāo)。單位為m。
相機(jī)坐標(biāo)系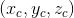 :在相機(jī)上建立的坐標(biāo)系,為了從相機(jī)的角度描述物體位置而定義,作為溝通世界坐標(biāo)系和圖像/像素坐標(biāo)系的中間一環(huán)。單位為m。
:在相機(jī)上建立的坐標(biāo)系,為了從相機(jī)的角度描述物體位置而定義,作為溝通世界坐標(biāo)系和圖像/像素坐標(biāo)系的中間一環(huán)。單位為m。
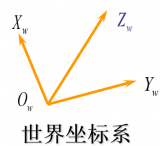
世界坐標(biāo)系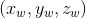 :用戶定義的三維世界的坐標(biāo)系,為了描述目標(biāo)物在真實(shí)世界里的位置而被引入。單位為m。
:用戶定義的三維世界的坐標(biāo)系,為了描述目標(biāo)物在真實(shí)世界里的位置而被引入。單位為m。
下面,我們來詳細(xì)推導(dǎo)從世界坐標(biāo)系到像素坐標(biāo)的過程。
世界坐標(biāo)系到相機(jī)坐標(biāo)系
從世界坐標(biāo)系到相機(jī)坐標(biāo)系, 這是一個剛體變換,只需對世界坐標(biāo)系的三維點(diǎn)作用一個旋轉(zhuǎn)R和平移t(R,t即為相機(jī)的外參),變換過程可以通過一下公式完成:
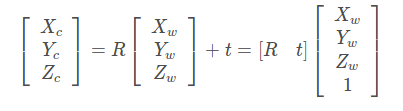
相機(jī)坐標(biāo)系到成像平面坐標(biāo)系
這一過程進(jìn)行了從三維坐標(biāo)到二維坐標(biāo)的轉(zhuǎn)換,也即投影透視過程(用中心投影法將物體投射到投影面上,從而獲得的一種較為接近視覺效果的單面投影圖,也就是使我們?nèi)搜劭吹骄拔锝筮h(yuǎn)小的一種成像方式)。
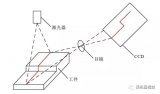
成像過程如下圖所示:針孔面(相機(jī)坐標(biāo)系)在圖像平面(圖像坐標(biāo)系)和物點(diǎn)平面(棋盤平面)之間,所成圖像為倒立實(shí)像。
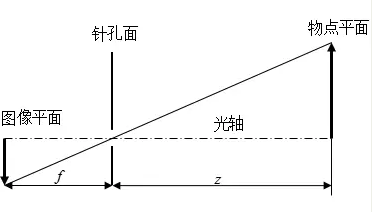
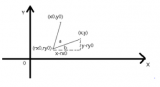
但是為了在數(shù)學(xué)上更方便描述,我們將相機(jī)坐標(biāo)系和圖像坐標(biāo)系位置對調(diào),變成下圖所示的布置方式(沒有實(shí)際的物理意義,只是方便計(jì)算):
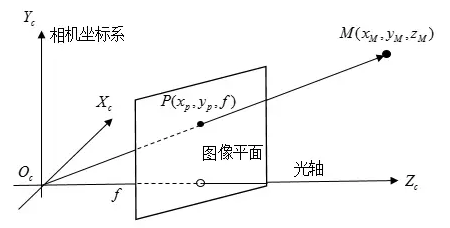
此時,假設(shè)相機(jī)坐標(biāo)系中有一點(diǎn)M,則在理想圖像坐標(biāo)系下(無畸變)的成像點(diǎn)P的坐標(biāo)為(可由相似三角形原則得出):
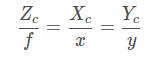
f為焦距,整理,得:
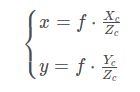
成像平面坐標(biāo)系到像素坐標(biāo)系
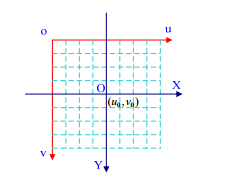
如上圖,成平面坐標(biāo)系和像素坐標(biāo)系之間存在一個縮放和平移
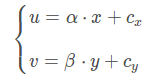
整理得:
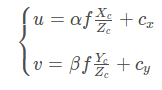
以fx、fy的方式表示為:
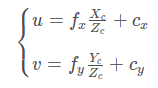
其中
α、β的單位為像素/米;
fx、fy為x、y方向的焦距,單位為像素;
(cx,cy)為主點(diǎn),圖像的中心,單位為像素。
那么,相機(jī)坐標(biāo)系到像素坐標(biāo)系的最終形式可寫成:
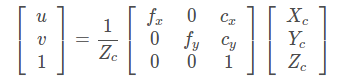
將 Zc移到左邊:
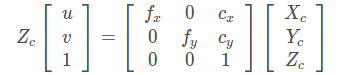
所以,在世界坐標(biāo)系中的三維點(diǎn)M=[X,Y,Z]T 和像素坐標(biāo)系中二維點(diǎn)m=[u,v]T的關(guān)系為:
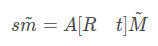
即:
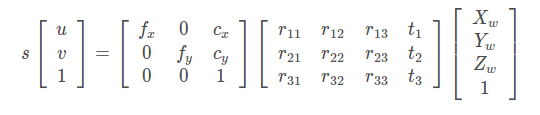
其中,s為縮放因子,A為相機(jī)的內(nèi)參矩陣,[R t]為相機(jī)的外參矩陣,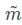 和
和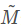 分別為m和M對應(yīng)的齊次坐標(biāo)。
分別為m和M對應(yīng)的齊次坐標(biāo)。
畸變模型
我們在攝像機(jī)坐標(biāo)系到圖像坐標(biāo)系變換時談到透視投影。攝像機(jī)拍照時通過透鏡把實(shí)物投影到像平面上,但是透鏡由于制造精度以及組裝工藝的偏差會引入畸變,導(dǎo)致原始圖像的失真。因此我們需要考慮成像畸變的問題。
透鏡的畸變主要分為徑向畸變和切向畸變,還有薄透鏡畸變等等,但都沒有徑向和切向畸變影響顯著,所以我們在這里只考慮徑向和切向畸變。
徑向畸變
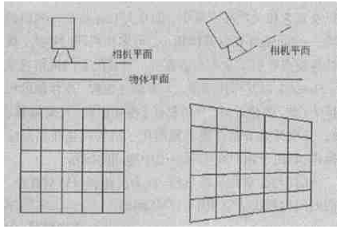
顧名思義,徑向畸變就是沿著透鏡半徑方向分布的畸變,產(chǎn)生原因是光線在原理透鏡中心的地方比靠近中心的地方更加彎曲,這種畸變在普通廉價(jià)的鏡頭中表現(xiàn)更加明顯,徑向畸變主要包括桶形畸變和枕形畸變兩種。以下分別是枕形和桶形畸變示意圖:
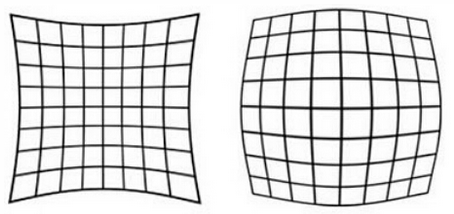
實(shí)際情況中我們常用r=0處的泰勒級數(shù)展開的前幾項(xiàng)來近似描述徑向畸變,矯正徑向畸變前后的坐標(biāo)關(guān)系為:
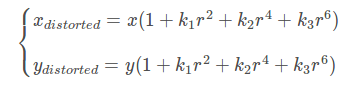
切向畸變
切向畸變是由于透鏡本身與相機(jī)傳感器平面(像平面)或圖像平面不平行而產(chǎn)生的,這種情況多是由于透鏡被粘貼到鏡頭模組上的安裝偏差導(dǎo)致。畸變模型可以用兩個額外的參數(shù)p1和p2來描述:
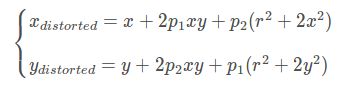
其中,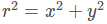
所以,我們一共需要5個畸變參數(shù)(k1,k2,k3,p1,p2)來描述透鏡畸變。
綜上所述,相機(jī)標(biāo)定實(shí)際上就是確定相機(jī)的內(nèi)外參數(shù)、畸變參數(shù)的過程。
以上是對于單個相機(jī)進(jìn)行標(biāo)定,那么對于多目相機(jī)系統(tǒng)或者RGBD 相機(jī)的標(biāo)定呢?
立體標(biāo)定
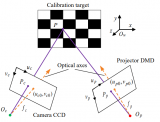
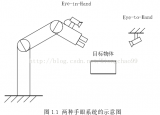
對于多目相機(jī)系統(tǒng)或者RGBD 相機(jī)除了要對別對每個相機(jī)進(jìn)行以上標(biāo)定以外,還需要求傳感器之間的變換T,以使同一時刻獲取的數(shù)據(jù)能夠“對齊”,以雙目為例,左右兩個相機(jī)的坐標(biāo)系如下圖:
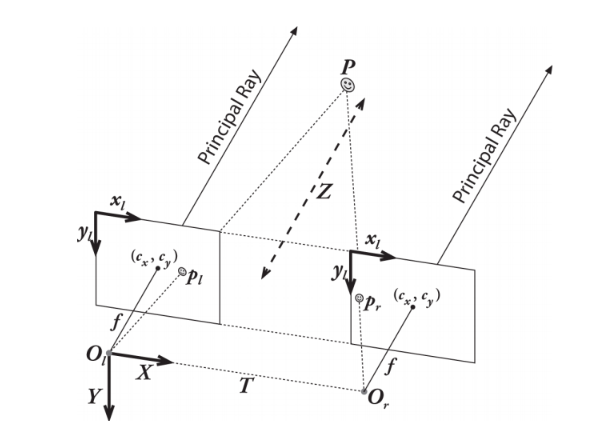
計(jì)算出兩個攝像機(jī)之間的旋轉(zhuǎn)矩陣R和平移向量t,方法是分別計(jì)算出兩個攝像機(jī)的R和T,再由以下公式計(jì)算: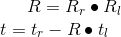
立體匹配
由于單相機(jī)獲取的圖像只能計(jì)算出二維坐標(biāo),因?yàn)槲覀兪褂昧?套相機(jī),且2套相機(jī)之間的關(guān)系也是已知的,那么如果我們能把三維空間中某點(diǎn)在左右相機(jī)成像的二維坐標(biāo)都計(jì)算出來,且能知道這是同一個點(diǎn),這樣就可以計(jì)算出三維坐標(biāo)。這里面確認(rèn)同名點(diǎn)的技術(shù)就是立體匹配。立體匹配有很多種算法,其中局部匹配法是最常用的,但是就目前已有算法來說,沒有一種算法可以實(shí)現(xiàn)100%匹配。一般來說待匹配點(diǎn)越多,匹配準(zhǔn)確率越低。
現(xiàn)有標(biāo)定方法介紹
相機(jī)標(biāo)定方法有:傳統(tǒng)相機(jī)標(biāo)定法、主動視覺相機(jī)標(biāo)定法、相機(jī)自標(biāo)定法。
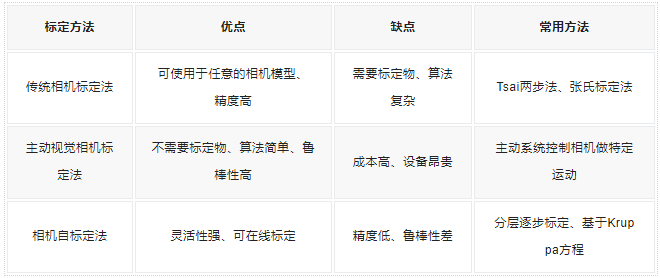
Tsai兩步法是先線性求得相機(jī)參數(shù),之后考慮畸變因素,得到初始的參數(shù)值,通過非線性優(yōu)化得到最終的相機(jī)參數(shù)。Tsai兩步法速度較快,但僅考慮徑向畸變,當(dāng)相機(jī)畸變嚴(yán)重時,該方法不適用。
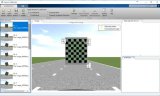
張氏標(biāo)定法使用二維方格組成的標(biāo)定板進(jìn)行標(biāo)定,采集標(biāo)定板不同位姿圖片,提取圖片中角點(diǎn)像素坐標(biāo),通過單應(yīng)矩陣計(jì)算出相機(jī)的內(nèi)外參數(shù)初始值,利用非線性最小二乘法估計(jì)畸變系數(shù),最后使用極大似然估計(jì)法優(yōu)化參數(shù)。該方法操作簡單,而且精度較高,可以滿足大部分場合。
基于主動視覺的相機(jī)標(biāo)定法是通過主動系統(tǒng)控制相機(jī)做特定運(yùn)動,利用控制平臺控制相機(jī)發(fā)生特定的移動拍攝多組圖像,依據(jù)圖像信息和已知位移變化來求解相機(jī)內(nèi)外參數(shù)。這種標(biāo)定方法需要配備精準(zhǔn)的控制平臺,因此成本較高。
分層逐步標(biāo)定法是先對圖像的序列做射影重建,在重建的基礎(chǔ)上進(jìn)行放射標(biāo)定和歐式標(biāo)定,通過非線性優(yōu)化算法求得相機(jī)內(nèi)外參數(shù)。由于初始參數(shù)是模糊值,優(yōu)化算法收斂性不確定。
基于Kruppa的自標(biāo)定法是通過二次曲線建立關(guān)于相機(jī)內(nèi)參矩陣的約束方程,至少使用3對圖像來標(biāo)定相機(jī)。圖像序列長度會影響標(biāo)定算法的穩(wěn)定性,無法保證射影空間中的無窮遠(yuǎn)平面。
以上為單個相機(jī)標(biāo)定的方法,而對于相機(jī)-相機(jī)、相機(jī)-距離傳感器之間進(jìn)行標(biāo)定,OpenCV、Matlab都有自帶的工具箱或函數(shù)庫可以用來標(biāo)定,但[1]提出了一個帶有Web界面的工具箱,用于全自動相機(jī)到相機(jī)和相機(jī)到范圍的校準(zhǔn)。該系統(tǒng)可在一分鐘內(nèi)恢復(fù)內(nèi)外參數(shù)以及攝像機(jī)和距離傳感器之間的轉(zhuǎn)換。而且,該方法所提出的基于生長的棋盤格角點(diǎn)檢測方法明顯優(yōu)于OpenCV需要指定棋盤格角點(diǎn)大小的角點(diǎn)檢測方法。
審核編輯:郭婷
 電子發(fā)燒友App
電子發(fā)燒友App










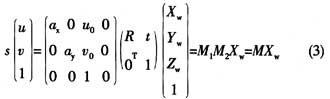
















評論