動態電路中無外施激勵電源,僅由動態元件初始儲能所產生的響應,稱為動態電路的零輸入響應。
RC電路的零輸入響應
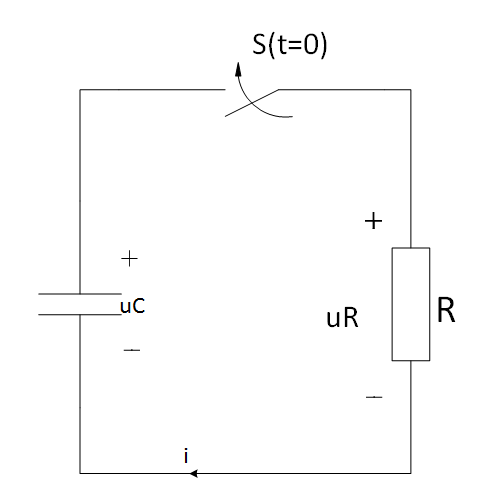
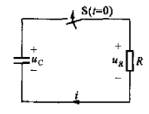
開關S閉合前,電容C已充電,其電壓uC=Uo。現把開關動作時刻取為計時起點(t=0)。開關閉合后,即t≥0+時,根據KVL可得
uR-uC=0
將uR=Ri(對R,電流、電壓的參考方向是關聯參考方向),i=-C(duC/dt)(對電容C,電流、電壓的參考方向是非關聯參考方向)代入上述方程,有
RC(duC/dt)+uC=0
(齊次線性方程dy/dx+P(x)y=0
通解為y=Ce-∫P(x)dx(C=±eC1)
對于RC(duC/dt)+uC=0,uC=Ae-∫(1/RC)dt=Ae-(1/RC)t
(RCp+1)Aept=0)
這是一階齊次微分方程,初始條件uC(0+)=uC(0-)=U0,令此方程的通解uC=Aept,代入上式后有
(RCp+1)Aept=0
相應的特征方程為
p=-(1/RC)
根據uC(0+)=uC(0-)=U0,以此代入uC=Aept,則可求得積分常數A=uC(0+)=U0。
電路中的電流為
i=(U0/R)e-(1/RC)t
電阻上的電壓
uR=uC=U0e-(1/R)t
由于p=-1/RC,這是電路特征方程的特征根,僅取決于電路的結構和元件的參數。當電阻的單位是Ω,電容的單位為F時,乘積RC的單位為s,它稱為RC電路的時間常數,用τ表示。引入τ后,電容電壓uC和電流i可以分別表示為
uC=U0e-t/τ
i=(U0/R)e-t/τ
RL電路的零輸入響應
過程與RC電路類似,從略
τ=L/R
i=I0e-t/τ
uR=RI0e-t/τ
uL=-RI0e-t/τ
-
動態電路
+關注
關注
1文章
27瀏覽量
9668 -
RC電路
+關注
關注
2文章
165瀏覽量
30822 -
激勵電源
+關注
關注
0文章
4瀏覽量
7577
發布評論請先 登錄





 動態電路中零輸入響應的一階齊次微分方程解析
動態電路中零輸入響應的一階齊次微分方程解析
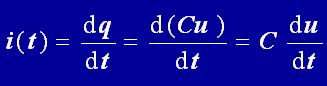
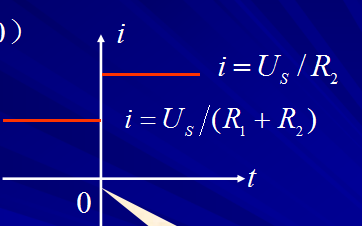
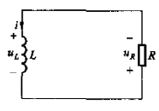










評論