本文討論了一種算法,用于在具有正交輸入向量的二維空間中找到最佳調(diào)整點。該算法根據(jù)測量數(shù)據(jù)點求解相交圓的方程。
幾個關鍵的系統(tǒng)性能指標由對應于幅度和相位的正交輸入?yún)?shù)確定;兩個例子是正交調(diào)制器載波饋通和邊帶抑制。這些參數(shù)通過優(yōu)化調(diào)制器正交基帶輸入之間的直流偏移平衡和幅度和相位平衡得到改善。
因為在給定二維空間的情況下找到這些參數(shù)的最優(yōu)調(diào)整并不是一件容易的事,所以在本文中,我將討論一種 Python 算法,用于在具有正交輸入向量的二維空間中找到最優(yōu)調(diào)整點。該算法根據(jù)測量數(shù)據(jù)點求解相交圓的方程,并在少至四次迭代中找到最佳點。為了舉例說明該技術,我使用了德州儀器 (TI) AFE7070集成數(shù)模轉(zhuǎn)換器 (DAC) 以及正交調(diào)制器載波饋通參數(shù)。
優(yōu)化雜散發(fā)射
通信系統(tǒng)努力將雜散發(fā)射降至最低。其中一些雜散發(fā)射源于正交輸入信號失配。例如,直流偏移失配和幅度/相位失衡將分別影響模擬正交調(diào)制器中的載波饋通和邊帶抑制參數(shù)。將輸入變量調(diào)整到最佳設定點可以最大限度地減少雜散輸出。
圖 1 將測量參數(shù)表示為從優(yōu)化點 [x0,y0] 到二維平面上實際點的矢量幅度 (r)。參數(shù)值以單位圓[0,1]為界。0 表示完全消除或無信號,1 表示無消除或完全信號。在分貝尺度中,該函數(shù)受 [-inf,0] 的約束。半徑為 r 的圓代表所有可能達到相同大小的 x,y 點。
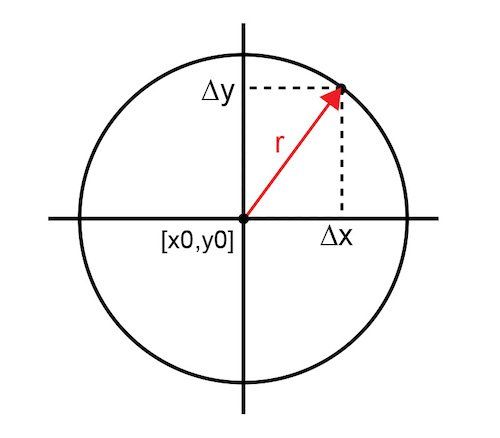
圖 1. 從優(yōu)化點到實際點的向量
等式 1 以最簡單的形式表示該函數(shù):
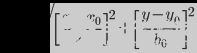
常數(shù) [a0,b0] 表示系統(tǒng)相關的歸一化因子,以保持最大結果小于 1。從技術上講,等式 1 描述了一個橢圓,因為每個自變量的比例因子不需要相同。為簡單起見,a0 等于 b0,因此曲線是真正的圓。
目標是盡快找到使測量參數(shù) (r) 最小化的最佳點 [x0,y0]。通過統(tǒng)計變化的輸入?yún)?shù)有效地找到該點具有挑戰(zhàn)性。傳統(tǒng)的狩獵和啄食方法使用連續(xù)試驗來縮小到最佳點。盡管這會產(chǎn)生所需的解決方案,但當收斂時間很關鍵時需要進行太多迭代,因此需要一種新方法。
相交的圓
理想情況下,使用相交圓的精確三個測量迭代確定最佳點。在任意輸入點 [x1,y1] 處的第一個測量結果定義了由半徑為 r1 的圓 A 表示的最優(yōu)點的無限可能性。添加第二個數(shù)據(jù)點會產(chǎn)生另一個由圓圈 B 表示的無限數(shù)據(jù)集;然而,兩個圓的交點將解縮小到兩點。第三個數(shù)據(jù)點和相應的圓 C 提供了第三條曲線,其中只有一個相互交叉點。該交點是最佳點。圖 2 顯示了最終確定最佳點的相交圓的進程。
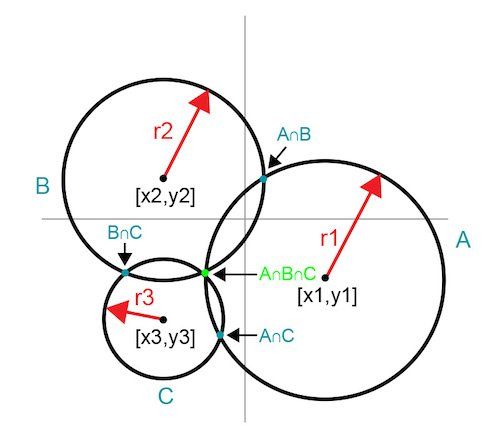
圖 2. 相交的圓揭示了一個共同的交點
這種技術在恰好三個迭代中揭示了最佳點。第四次迭代測量最佳點以確認和記錄結果。
圖 3 說明了一種通過使用 xy 平面中經(jīng)驗已知的邊界信息來消除一次迭代的技術。在其中一個邊界點處選擇初始點,使第一條曲線 (A) 為 90 度圓弧。通過沿 x 或 y 方向移動選擇第一個弧上的第二個點。
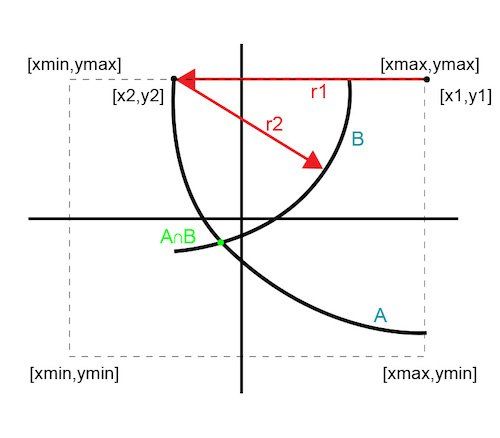
圖 3. 兩次迭代解決方案
由于第二個點仍然在邊界邊上,所以它的曲線是一個低于 180 度的弧。這兩條曲線的交點提供了一個最佳點。這種方法僅在兩次迭代中就揭示了最佳點,并通過三次來確認。
逐次圓逼近
最優(yōu)解取決于數(shù)學方程的準確性。在實際測量情況下,一些假設或錯誤會影響結果。測量的信號非常小;噪聲和測量容差會引入誤差。使用完美的圓而不是橢圓會引入一些不確定性。求解多個方程所需的比例因子假設也引入了不確定性。這些錯誤和假設轉(zhuǎn)化為曲線的模糊性。
圖 4 說明了模糊曲線如何不能保證精確的交點;相反,它們定義了一個收斂區(qū)域。
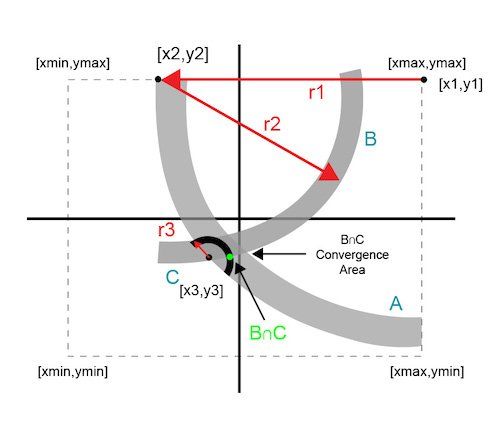
圖 4. 連續(xù)圓相交近似
每個附加數(shù)據(jù)點都使用上一次迭代的數(shù)據(jù)。連續(xù)的圓圈會聚到系統(tǒng)最小閾值內(nèi)的解決方案區(qū)域。
測量示例
該示例使用 AFE7070 DAC 并針對載波饋通參數(shù)進行優(yōu)化。AFE7070 是一個方便的平臺,因為集成了 DAC 和調(diào)制器。調(diào)制器正交輸入上的 DC 失調(diào)不平衡決定了載波饋通性能。AFE7070 具有內(nèi)部數(shù)字調(diào)諧功能,可精確控制 DC 偏移平衡。不需要太多;分辨率為微伏級。
該示例的 x,y 參數(shù)是整數(shù)數(shù)字階躍值,用于控制正交輸入上的 DC 電平。設備的先前統(tǒng)計采樣提供了輸入變量的 x、y 范圍以及計算中使用的步驟表。步進表提供了以分貝毫瓦為單位的測量載波饋通到 delta-x(或 delta-y)因子的“轉(zhuǎn)換”。
高(或換句話說,差)測量值意味著設置偏離并且需要更大的增量才能達到最佳點。相反,低值意味著設定點接近并且需要進行小的修正。這一點“功課”對于確保初始猜測點不會太遠,并將迭代時間減少到最低限度是必要的。
圖 5 顯示了 Python 算法,它在四次或更少的迭代中找到最佳輸入變量。

圖 5. Python 優(yōu)化算法
函數(shù)“Get_r”和“GetCFi”是特定于設備的測量。為簡潔起見,我省略了代碼,因為它對于演示優(yōu)化算法無關緊要。在您的應用程序中,這些功能與系統(tǒng)中設備參數(shù)的編程和測量有關。
結論
對于 AFE7070 DAC,在大多數(shù)情況下,該算法可在 3 次迭代內(nèi)優(yōu)化載波饋通,并在不到 1.7 秒內(nèi)優(yōu)化,主要由頻譜分析儀建立和掃描時間進行選通。之前的步驟方法需要近 20 次迭代和 20 多秒才能完成。與傳統(tǒng)方法相比,該算法的速度提高了 10 倍以上。依賴于增益和相位的正交輸入變量的其他通信系統(tǒng)參數(shù)也可以使用該算法來有效地找到最優(yōu)解。
-
算法
+關注
關注
23文章
4705瀏覽量
95119 -
通信系統(tǒng)
+關注
關注
6文章
1225瀏覽量
54052
發(fā)布評論請先 登錄
一種適用于無線通信系統(tǒng)的半盲ICA算法
一文解析Vue代碼層面的優(yōu)化
多目標優(yōu)化算法有哪些
用于全局優(yōu)化的混合正交遺傳算法
網(wǎng)絡監(jiān)管系統(tǒng)爬網(wǎng)算法優(yōu)化
參數(shù)優(yōu)化模型的正交逼近算法
高階FIR正交鏡像濾波器的設計
基于機器學習算法的SVM優(yōu)化
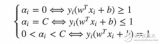
剖析正交匹配追蹤算法的優(yōu)化設計與FPGA實現(xiàn)

基于LSPIA的NURBS曲線擬合優(yōu)化算法

300M鋼正交切削加工變量相關實驗測試






 一文解析通信系統(tǒng)的高效正交變量優(yōu)化算法
一文解析通信系統(tǒng)的高效正交變量優(yōu)化算法











評論