1 貝葉斯定理

1.1 幾個概率定義

先驗概率(邊緣概率)：某個事件發(fā)生的概率，通常是在沒有條件約束下事物的客觀發(fā)生概率，比如拋硬幣的50%概率

后驗概率(條件概率)：一個事件在另一個事件已經(jīng)發(fā)生的條件下的發(fā)生概率

1.2 條件概率公式和全概率公式

條件概率公式：

全概率公式：

1.3 貝葉斯公式

貝葉斯公式可以簡單的通過條件概率公式和全概率公式推出：

可以簡寫成：

2 貝葉斯定理的含義

我們可以將貝葉斯公式寫成：

其中，P(A)為事件A發(fā)生的先驗概率，為事件A發(fā)生的后驗概率，稱為似然函數(shù)，它可以看作一個調(diào)整因子，它通過對先驗概率進行調(diào)整，使其更加接近真實概率。

故貝葉斯公式可以理解為：

后驗概率 = 先驗概率似然函數(shù)

貝葉斯定理的含義也就是：為了估測一個事件A的真實概率，我們對該事件加入一個實驗結(jié)果，即似然函數(shù)，當(dāng)似然函數(shù)大于1，則先驗概率被增強，A事件發(fā)生可能性變大：當(dāng)似然函數(shù)小于1，則先驗概率被削弱，A事件發(fā)生可能性變小。

3 一個例子

eg.已知某種疾病的發(fā)病率為0.001，即1000個人中會有1個人得病。現(xiàn)有一種試劑可以檢測患者是否得病，它的準(zhǔn)確率為0.99，即在患者得病的情況下，它有0.99的可能性呈陽性。它的誤報率為5%，即患者在沒有得病的情況下，它也會有5%的可能性呈陽性。現(xiàn)有一個病人的檢驗結(jié)果為陽性，請問他確實得病的可能性有多大？

解：定義事件A為患者得病，事件B為檢驗結(jié)果陽性。
所以我們要計算的為。
利用貝葉斯公式：

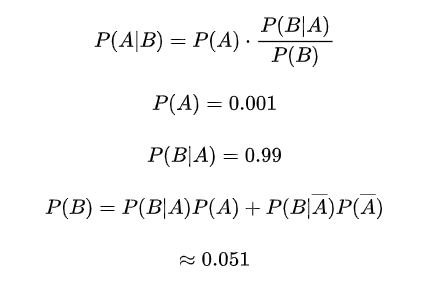
可知，檢查結(jié)果為陽性患病可能性也并不大，即“假陽性”。

審核編輯 ：李倩