隨機(jī)森林是以決策樹(shù)為基學(xué)習(xí)器的集成學(xué)習(xí)算法。隨機(jī)森林非常簡(jiǎn)單,易于實(shí)現(xiàn),計(jì)算開(kāi)銷(xiāo)也很小,更令人驚奇的是它在分類(lèi)和回歸上表現(xiàn)出了十分驚人的性能,因此,隨機(jī)森林也被譽(yù)為“代表集成學(xué)習(xí)技術(shù)水平的方法”。
一、隨機(jī)森林RF簡(jiǎn)介
只要了解決策樹(shù)的算法,那么隨機(jī)森林是相當(dāng)容易理解的。隨機(jī)森林的算法可以用如下幾個(gè)步驟概括:
用有抽樣放回的方法(bootstrap)從樣本集中選取n個(gè)樣本作為一個(gè)訓(xùn)練集。
用抽樣得到的樣本集生成一棵決策樹(shù)。在生成的每一個(gè)結(jié)點(diǎn):
隨機(jī)不重復(fù)地選擇d個(gè)特征;
利用這d個(gè)特征分別對(duì)樣本集進(jìn)行劃分,找到最佳的劃分特征(可用基尼系數(shù)、增益率或者信息增益判別)。
重復(fù)步驟1到步驟2共k次,k即為隨機(jī)森林中決策樹(shù)的個(gè)數(shù)。
用訓(xùn)練得到的隨機(jī)森林對(duì)測(cè)試樣本進(jìn)行預(yù)測(cè),并用票選法決定預(yù)測(cè)的結(jié)果。
下圖比較直觀地展示了隨機(jī)森林算法(圖片出自文獻(xiàn)2):
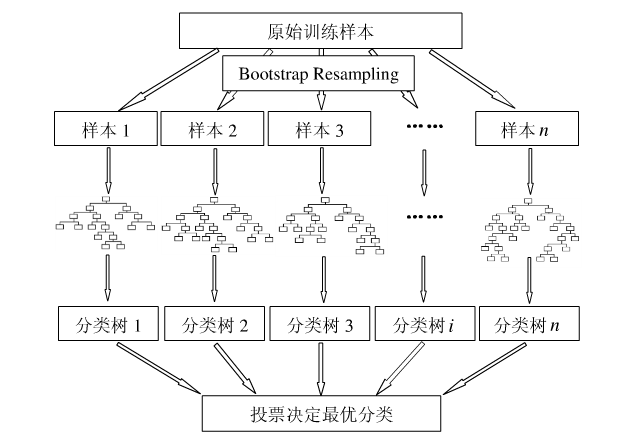
圖1:隨機(jī)森林算法示意圖
沒(méi)錯(cuò),就是這個(gè)到處都是隨機(jī)取值的算法,在分類(lèi)和回歸上有著極佳的效果,是不是覺(jué)得強(qiáng)的沒(méi)法解釋~
然而本文的重點(diǎn)不是這個(gè),而是接下來(lái)的特征重要性評(píng)估。
二、特征重要性評(píng)估
現(xiàn)實(shí)情況下,一個(gè)數(shù)據(jù)集中往往有成百上前個(gè)特征,如何在其中選擇比結(jié)果影響最大的那幾個(gè)特征,以此來(lái)縮減建立模型時(shí)的特征數(shù)是我們比較關(guān)心的問(wèn)題。這樣的方法其實(shí)很多,比如主成分分析,lasso等等。不過(guò),這里我們要介紹的是用隨機(jī)森林來(lái)對(duì)進(jìn)行特征篩選。
用隨機(jī)森林進(jìn)行特征重要性評(píng)估的思想其實(shí)很簡(jiǎn)單,說(shuō)白了就是看看每個(gè)特征在隨機(jī)森林中的每棵樹(shù)上做了多大的貢獻(xiàn),然后取個(gè)平均值,最后比一比特征之間的貢獻(xiàn)大小。
好了,那么這個(gè)貢獻(xiàn)是怎么一個(gè)說(shuō)法呢?通常可以用基尼指數(shù)(Gini index)或者袋外數(shù)據(jù)(OOB)錯(cuò)誤率作為評(píng)價(jià)指標(biāo)來(lái)衡量。
我們這里只介紹用基尼指數(shù)來(lái)評(píng)價(jià)的方法,首先對(duì)另一種方法做個(gè)簡(jiǎn)單介紹。
的定義為:在 RF 的每棵樹(shù)中,使用隨機(jī)抽取的訓(xùn)練自助樣本建樹(shù),并計(jì)算袋外數(shù)據(jù) OOB)的預(yù)測(cè)錯(cuò)誤率,然后隨機(jī)置換變量X,的觀測(cè)值后再次建樹(shù)并計(jì)算 OOB 的預(yù)測(cè)錯(cuò)誤率,最后計(jì)算兩次 OOB 錯(cuò)誤率的差值經(jīng)過(guò)標(biāo)準(zhǔn)化處理后在所有樹(shù)中的平均值即為變量 ,的置換重要性 ()
我們將變量重要性評(píng)分(variable importance measures)用 來(lái)表示,將Gini指數(shù)用 來(lái)表示,假設(shè)有 個(gè)特征 ,,,,, 棵決策樹(shù), 個(gè)類(lèi)別,現(xiàn)在要計(jì)算出每個(gè)特征 的Gini指數(shù)評(píng)分 ,亦即第 個(gè)特征在RF所有決策樹(shù)中節(jié)點(diǎn)分裂不純度的平均改變量。
第 棵樹(shù)節(jié)點(diǎn) 的 指數(shù)的計(jì)算公式為:
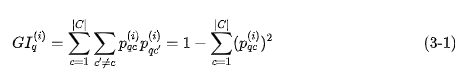
其中, 表示有 個(gè)類(lèi)別, 表示節(jié)點(diǎn) 中類(lèi)別 所占的比例。直觀地說(shuō),就是隨便從節(jié)點(diǎn) 中隨機(jī)抽取兩個(gè)樣本,其類(lèi)別標(biāo)記不一致的概率。
特征 在第 棵樹(shù)節(jié)點(diǎn) 的重要性,即節(jié)點(diǎn) 分枝前后的 指數(shù)變化量為:
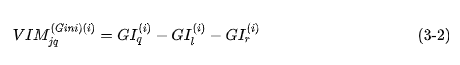
其中,和 分別表示分枝后兩個(gè)新節(jié)點(diǎn)的指數(shù)。如果,特征 在決策樹(shù) i 中出現(xiàn)的節(jié)點(diǎn)為集合,那么 在第 棵樹(shù)的重要性為:

三、舉個(gè)例子
值得慶幸的是,sklearn已經(jīng)幫我們封裝好了一切,我們只需要調(diào)用其中的函數(shù)即可。
我們以UCI上葡萄酒的例子為例,首先導(dǎo)入數(shù)據(jù)集。
importpandasaspd
url='http://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data'
df=pd.read_csv(url,header=None)
df.columns=['Classlabel','Alcohol','Malicacid','Ash',
'Alcalinityofash','Magnesium','Totalphenols',
'Flavanoids','Nonflavanoidphenols','Proanthocyanins',
'Colorintensity','Hue','OD280/OD315ofdilutedwines','Proline']
然后,我們來(lái)大致看下這時(shí)一個(gè)怎么樣的數(shù)據(jù)集
importnumpyasnp
np.unique(df['Classlabel'])
輸出為
array([1,2,3],dtype=int64)
可見(jiàn)共有3個(gè)類(lèi)別。然后再來(lái)看下數(shù)據(jù)的信息:
df.info()
輸出為
RangeIndex: 178 entries, 0 to 177
Data columns (total 14 columns):
Class label 178 non-null int64
Alcohol 178 non-null float64
Malic acid 178 non-null float64
Ash 178 non-null float64
Alcalinity of ash 178 non-null float64
Magnesium 178 non-null int64
Total phenols 178 non-null float64
Flavanoids 178 non-null float64
Nonflavanoid phenols 178 non-null float64
Proanthocyanins 178 non-null float64
Color intensity 178 non-null float64
Hue 178 non-null float64
OD280/OD315 of diluted wines 178 non-null float64
Proline 178 non-null int64
dtypes: float64(11), int64(3)
memory usage: 19.5 KB
可見(jiàn)除去class label之外共有13個(gè)特征,數(shù)據(jù)集的大小為178。
按照常規(guī)做法,將數(shù)據(jù)集分為訓(xùn)練集和測(cè)試集。
try:
fromsklearn.cross_validationimporttrain_test_split
except:
fromsklearn.model_selectionimporttrain_test_split
fromsklearn.ensembleimportRandomForestClassifier
x,y=df.iloc[:,1:].values,df.iloc[:,0].values
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=0)
feat_labels=df.columns[1:]
forest=RandomForestClassifier(n_estimators=10000,random_state=0,n_jobs=-1)
forest.fit(x_train,y_train)
好了,這樣一來(lái)隨機(jī)森林就訓(xùn)練好了,其中已經(jīng)把特征的重要性評(píng)估也做好了,我們拿出來(lái)看下。
importances=forest.feature_importances_
indices=np.argsort(importances)[::-1]
forfinrange(x_train.shape[1]):
print("%2d)%-*s%f"%(f+1,30,feat_labels[indices[f]],importances[indices[f]]))
輸出的結(jié)果為
1) Color intensity 0.182483
2) Proline 0.158610
3) Flavanoids 0.150948
4) OD280/OD315 of diluted wines 0.131987
5) Alcohol 0.106589
6) Hue 0.078243
7) Total phenols 0.060718
8) Alcalinity of ash 0.032033
9) Malic acid 0.025400
10) Proanthocyanins 0.022351
11) Magnesium 0.022078
12) Nonflavanoid phenols 0.014645
13) Ash 0.013916
對(duì)的就是這么方便。
如果要篩選出重要性比較高的變量的話,這么做就可以
threshold=0.15
x_selected=x_train[:,importances>threshold]
x_selected.shape
輸出為
(124, 3)
瞧,這不,幫我們選好了3個(gè)重要性大于0.15的特征了嗎~
審核編輯:郭婷
-
RF
+關(guān)注
關(guān)注
65文章
3175瀏覽量
168779 -
數(shù)據(jù)集
+關(guān)注
關(guān)注
4文章
1223瀏覽量
25384
原文標(biāo)題:利用隨機(jī)森林評(píng)估特征重要性原理與應(yīng)用
文章出處:【微信號(hào):vision263com,微信公眾號(hào):新機(jī)器視覺(jué)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
GPS產(chǎn)業(yè)的發(fā)展和重要性與日俱增
基于隨機(jī)森林模型下CINI的RFG-SVM
隨機(jī)森林的跌倒檢測(cè)算法
面向HC256,RC4利用NOST進(jìn)行系統(tǒng)隨機(jī)性檢測(cè)
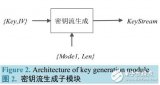
基于遺傳算法和隨機(jī)森林的XGBoost改進(jìn)方法
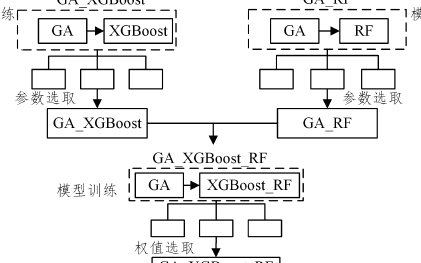
面向差分?jǐn)?shù)據(jù)挖掘隱私保護(hù)的隨機(jī)森林算法
基于特征切分和隨機(jī)森林的異常點(diǎn)檢測(cè)模型
基于加權(quán)隨機(jī)森林等的惡意軟件檢測(cè)
Python如何進(jìn)行特征重要性分析

Python中進(jìn)行特征重要性分析的9個(gè)常用方法
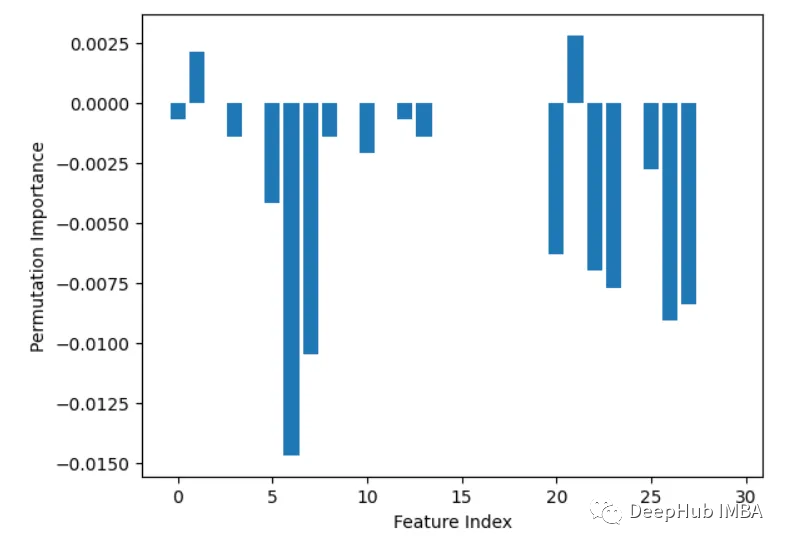
什么是隨機(jī)森林?隨機(jī)森林的工作原理





 利用隨機(jī)森林進(jìn)行特征重要性評(píng)估
利用隨機(jī)森林進(jìn)行特征重要性評(píng)估











評(píng)論