作者 | 京東云開發者-京東物流 紀卓志

目前市面上充斥著大量關于跳躍表結構與 Redis 的源碼解析，但是經過長期觀察后發現大都只是在停留在代碼的表面，而沒有系統性地介紹跳躍表的由來以及各種常量的由來。作為一種概率數據結構，理解各種常量的由來可以更好地進行變化并應用到高性能功能開發中。本文沒有重復地以對現有優秀實現進行代碼分析，而是通過對跳躍表進行了系統性地介紹與形式化分析，并給出了在特定場景下的跳躍表擴展方式，方便讀者更好地理解跳躍表數據結構。

跳躍表 [1,2,3] 是一種用于在大多數應用程序中取代平衡樹的概率數據結構。跳躍表擁有與平衡樹相同的期望時間上界，并且更簡單、更快、是用更少的空間。在查找與列表的線性操作上，比平衡樹更快，并且更簡單。

概率平衡也可以被用在基于樹的數據結構 [4] 上，例如樹堆（Treap）。與平衡二叉樹相同，跳躍表也實現了以下兩種操作

通過搜索引用 [5]，可以保證從任意元素開始，搜索到在列表中間隔為 k 的元素的任意期望時間是 O (logk)

實現線性表的常規操作（例如_將元素插入到列表第 k 個元素后面_）

這幾種操作在平衡樹中也可以實現，但是在跳躍表中實現起來更簡單而且非常的快，并且通常情況下很難在平衡樹中直接實現（樹的線索化可以實現與鏈表相同的效果，但是這使得實現變得更加復雜 [6]）

預覽

最簡單的支持查找的數據結構可能就是鏈表。Figure.1 是一個簡單的鏈表。在鏈表中執行一次查找的時間正比于必須考查的節點個數，這個個數最多是 N。

Figure.1 Linked List

Figure.2 表示一個鏈表，在該鏈表中，每個一個節點就有一個附加的指針指向它在表中的前兩個位置上的節點。正因為這個前向指針，在最壞情況下最多考查?N/2?+1 個節點。

Figure.2 Linked List with fingers to the 2nd forward elements

Figure.3 將這種想法擴展，每個序數是 4 的倍數的節點都有一個指針指向下一個序數為 4 的倍數的節點。只有?N/4?+2 個節點被考查。

Figure.3 Linked List with fingers to the 4th forward elements

這種跳躍幅度的一般情況如 Figure.4 所示。每個 2i 節點就有一個指針指向下一個 2i 節點，前向指針的間隔最大為 N/2。可以證明總的指針最大不會超過 2N（見空間復雜度分析），但現在在一次查找中最多考查?logN?個節點。這意味著一次查找中總的時間消耗為 O (logN)，也就是說在這種數據結構中的查找基本等同于二分查找（binary search）。

Figure.4 Linked List with fingers to the 2ith forward elements

在這種數據結構中，每個元素都由一個節點表示。每個節點都有一個高度（height）或級別（level），表示節點所擁有的前向指針數量。每個節點的第 i 個前向指針指向下一個級別為 i 或更高的節點。

在前面描述的數據結構中，每個節點的級別都是與元素數量有關的，當插入或刪除時需要對數據結構進行調整來滿足這樣的約束，這是很呆板且低效的。為此，可以_將每個 2i 節點就有一個指針指向下一個 2i 節點_的限制去掉，當新元素插入時為每個新節點分配一個隨機的級別而不用考慮數據結構的元素數量。

Figure.5 Skip List

數據結構

到此為止，已經得到了所有讓鏈表支持快速查找的充要條件，而這種形式的數據結構就是跳躍表。接下來將會使用更正規的方式來定義跳躍表

所有元素在跳躍表中都是由一個節點表示。

每個節點都有一個高度或級別，有時候也可以稱之為階（step），節點的級別是一個與元素總數無關的隨機數。規定 NULL 的級別是∞。

每個級別為 k 的節點都有 k 個前向指針，且第 i 個前向指針指向下一個級別為 i 或更高的節點。

每個節點的級別都不會超過一個明確的常量 MaxLevel。整個跳躍表的級別是所有節點的級別的最高值。如果跳躍表是空的，那么跳躍表的級別就是 1。

存在一個頭節點 head，它的級別是 MaxLevel，所有高于跳躍表的級別的前向指針都指向 NULL。

稍后將會提到，節點的查找過程是在頭節點從最高級別的指針開始，沿著這個級別一直走，直到找到大于正在尋找的節點的下一個節點（或者是 NULL），在此過程中除了頭節點外并沒有使用到每個節點的級別，因此每個節點無需存儲節點的級別。

在跳躍表中，級別為 1 的前向指針與原始的鏈表結構中 next 指針的作用完全相同，因此跳躍表支持所有鏈表支持的算法。

對應到高級語言中的結構定義如下所示（后續所有代碼示例都將使用 C 語言描述）

#define SKIP_LIST_KEY_TYPE     int
#define SKIP_LIST_VALUE_TYPE   int
#define SKIP_LIST_MAX_LEVEL    32
#define SKIP_LIST_P            0.5

struct Node {
  SKIP_LIST_KEY_TYPE    key;
  SKIP_LIST_VALUE_TYPE  value;
  struct Node          *forwards[]; // flexible array member
};

struct SkipList {
  struct Node *head;
  int          level;
};

struct Node *CreateNode(int level) {
  struct Node *node;
  assert(level > 0);
  node = malloc(sizeof(struct Node) + sizeof(struct Node *) * level);
  return node;
}

struct SkipList *CreateSkipList() {
  struct SkipList *list;
  struct Node     *head;
  int              i;

  list = malloc(sizeof(struct SkipList));
  head = CreateNode(SKIP_LIST_MAX_LEVEL);
  for (i = 0; i < SKIP_LIST_MAX_LEVEL; i++) {
    head->forwards[i] = NULL;
  }
  list->head = head;
  list->level = 1;

  return list;
}

從前面的預覽章節中，不難看出 MaxLevel 的選值影響著跳躍表的查詢性能，關于 MaxLevel 的選值將會在后續章節中進行介紹。在此先將 MaxLevel 定義為 32，這對于 232 個元素的跳躍表是足夠的。延續預覽章節中的描述，跳躍表的概率被定義為 0.5，關于這個值的選取問題將會在后續章節中進行詳細介紹。

算法

搜索

在跳躍表中進行搜索的過程，是通過 Z 字形遍歷所有沒有超過要尋找的目標元素的前向指針來完成的。在當前級別沒有可以移動的前向指針時，將會移動到下一級別進行搜索。直到在級別為 1 的時候且沒有可以移動的前向指針時停止搜索，此時直接指向的節點（級別為 1 的前向指針）就是包含目標元素的節點（如果目標元素在列表中的話）。在 Figure.6 中展示了在跳躍表中搜索元素 17 的過程。


Figure.6 A search path to find element 17 in Skip List 整個過程的示例代碼如下所示，因為高級語言中的數組下標從 0 開始，因此 forwards [0] 表示節點的級別為 1 的前向指針，依此類推

struct Node *SkipListSearch(struct SkipList *list, SKIP_LIST_KEY_TYPE target) {
  struct Node *current;
  int          i;

  current = list->head;
  for (i = list->level - 1; i >= 0; i--) {
    while (current->forwards[i] && current->forwards[i]->key < target) {
      current = current->forwards[i];
    }
  }

  current = current->forwards[0];
  if (current->key == target) {
    return current;
  } else {
    return NULL;
  }
}

插入和刪除

在插入和刪除節點的過程中，需要執行和搜索相同的邏輯。在搜索的基礎上，需要維護一個名為 update 的向量，它維護的是搜索過程中跳躍表每個級別上遍歷到的最右側的值，表示插入或刪除的節點的左側直接直接指向它的節點，用于在插入或刪除后調整節點所在所有級別的前向指針（與樸素的鏈表節點插入或刪除的過程相同）。 當新插入節點的級別超過當前跳躍表的級別時，需要增加跳躍表的級別并將 update 向量中對應級別的節點修改為 head 節點。 Figure.7 和 Figure.8 展示了在跳躍表中插入元素 16 的過程。首先，在 Figure.7 中執行與搜索相同的查詢過程，在每個級別遍歷到的最后一個元素在對應層級的前向指針被標記為灰色，表示稍后將會對齊進行調整。接下來在 Figure.8 中，在元素為 13 的節點后插入元素 16，元素 16 對應的節點的級別是 5，這比跳躍表當前級別要高，因此需要增加跳躍表的級別到 5，并將 head 節點對應級別的前向指針標記為灰色。Figure.8 中所有虛線部分都表示調整后的效果。

Figure.7 Search path for inserting element 16



Figure.8 Insert element 16 and adjust forward pointers

struct Node *SkipListInsert(struct SkipList *list, SKIP_LIST_KEY_TYPE key, SKIP_LIST_VALUE_TYPE value) {
  struct Node *update[SKIP_LIST_MAX_LEVEL];
  struct Node *current;
  int          i;
  int          level;

  current = list->head;
  for (i = list->level - 1; i >= 0; i--) {
    while (current->forwards[i] && current->forwards[i]->key < target) {
      current = current->forwards[i];
    }
    update[i] = current;
  }

  current = current->forwards[0];
  if (current->key == target) {
    current->value = value;
    return current;
  }

  level = SkipListRandomLevel();
  if (level > list->level) {
    for (i = list->level; i < level; i++) {
      update[i] = list->header;
    }
  }

  current = CreateNode(level);
  current->key = key;
  current->value = value;

  for (i = 0; i < level; i++) {
    current->forwards[i] = update[i]->forwards[i];
    update[i]->forwards[i] = current;
  }

  return current;
}

在刪除節點后，如果刪除的節點是跳躍表中級別最大的節點，那么需要降低跳躍表的級別。 Figure.9 和 Figure.10 展示了在跳躍表中刪除元素 19 的過程。首先，在 Figure.9 中執行與搜索相同的查詢過程，在每個級別遍歷到的最后一個元素在對應層級的前向指針被標記為灰色，表示稍后將會對齊進行調整。接下來在 Figure.10 中，首先通過調整前向指針將元素 19 對應的節點從跳躍表中卸載，因為元素 19 對應的節點是級別最高的節點，因此將其從跳躍表中移除后需要調整跳躍表的級別。Figure.10 中所有虛線部分都表示調整后的效果。 Figure.9 Search path for deleting element 19 Figure.10 Delete element 19 and adjust forward pointers

struct Node *SkipListDelete(struct SkipList *list, SKIP_LIST_KEY_TYPE key) {
  struct Node *update[SKIP_LIST_MAX_LEVEL];
  struct Node *current;
  int          i;

  current = list->head;
  for (i = list->level - 1; i >= 0; i--) {
    while (current->forwards[i] && current->forwards[i]->key < key) {
      current = current->forwards[i];
    }
    update[i] = current;
  }

  current = current->forwards[0];
  if (current && current->key == key) {
    for (i = 0; i < list->level; i++) {
      if (update[i]->forwards[i] == current) {
        update[i]->forwards[i] = current->forwards[i];
      } else {
        break;
      }
    }

    while (list->level > 1 && list->head->forwards[list->level - 1] == NULL) {
      list->level--;
    }
  }

  return current;
}

生成隨機級別

int SkipListRandomLevel() {
  int level;
  level = 1;
  while (random() < RAND_MAX * SKIP_LIST_P && level <= SKIP_LIST_MAX_LEVEL) {
    level++;
  }
  return level;
}

以下表格為按上面算法執行 232 次后，所生成的隨機級別的分布情況。

1	2	3	4	5	6	7	8
2147540777	1073690199	536842769	268443025	134218607	67116853	33563644	16774262
9	10	11	12	13	14	15	16
8387857	4193114	2098160	1049903	523316	262056	131455	65943
17	18	19	20	21	22	23	24
32611	16396	8227	4053	2046	1036	492	249
25	26	27	28	29	30	31	32
121	55	34	16	7	9	2	1

MaxLevel 的選擇

在 Figure.4 中曾給出過對于 10 個元素的跳躍表最理想的分布情況，其中 5 個節點的級別是 1，3 個節點的級別是 2，1 個節點的級別是 3，1 個節點的級別是 4。 這引申出一個問題：既然相同元素數量下，跳躍表的級別不同會有不同的性能，那么跳躍表的級別為多少才合適？

分析

空間復雜度分析

前面提到過，分數 p 代表節點同時帶有第 i 層前向指針和第 i+1 層前向指針的概率，而每個節點的級別最少是 1，因此級別為 i 的前向指針數為 npi?1。定義 S (n) 表示所有前向指針的總量，由等比數列求和公式可得 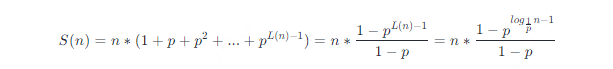對 S (n) 求極限，有 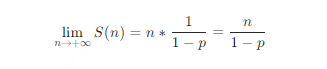易證，這是一個關于 p 的單調遞增函數，因此 p 的值越大，跳躍表中前向指針的總數越多。因為 1?p 是已知的常數，所以說跳躍表的空間復雜度是 O (n)。

時間復雜度分析

非形式化分析

形式化分析

延續_分數 p 代表節點同時帶有第 i 層前向指針和第 i+1 層前向指針的概率_的定義，考慮反方向分析搜索路徑。 搜索的路徑總是小于必須執行的比較的次數的。首先需要考查從級別 1（在搜索到元素前遍歷的最后一個節點）爬升到級別 L (n) 所需要反向跟蹤的指針數量。雖然在搜索時可以確定每個節點的級別都是已知且確定的，在這里仍認為只有當整個搜索路徑都被反向追蹤后才能被確定，并且在爬升到級別 L (n) 之前都不會接觸到 head 節點。 在爬升過程中任何特定的點，都認為是在元素 x 的第 i 個前向指針，并且不知道元素 x 左側所有元素的級別或元素 x 的級別，但是可以知道元素 x 的級別至少是 i。元素 x 的級別大于 i 的概率是 p，可以通過考慮視認為這個反向爬升的過程是一系列由成功的爬升到更高級別或失敗地向左移動的隨機獨立實驗。 在爬升到級別 L (n) 過程中，向左移動的次數等于在連續隨機試驗中第 L (n)?1 次成功前的失敗的次數，這符合負二項分布。期望的向上移動次數一定是 L (n)?1。因此可以得到無限列表中爬升到 L (n) 的代價 C C=prob (L (n)?1)+NB (L (n)?1,p) 列表長度無限大是一個悲觀的假設。當反向爬升的過程中接觸到 head 節點時，可以直接向上爬升而不需要任何向左移動。因此可以得到 n 個元素列表中爬升到 L (n) 的代價 C (n) C(n)≤probC=prob(L(n)?1)+NB(L(n)?1,p) 因此 n 個元素列表中爬升到 L (n) 的代價 C (n) 的數學期望和方差為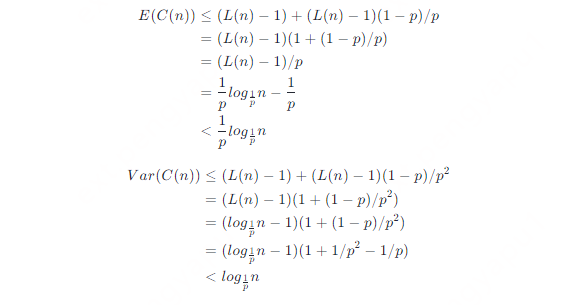

因為 1/p 是已知常數，因此跳躍表的搜索、插入和刪除的時間復雜度都是 O (logn)。

P 的選擇

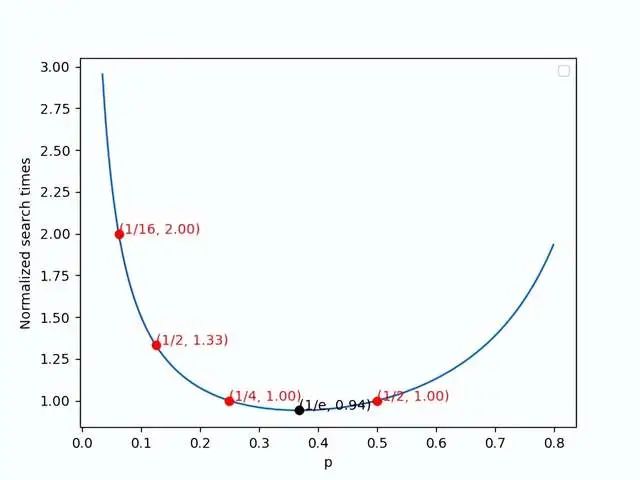
Figure.11 Normalized search times

擴展

快速隨機訪問

#define SKIP_LIST_KEY_TYPE     int
#define SKIP_LIST_VALUE_TYPE   int
#define SKIP_LIST_MAX_LEVEL    32
#define SKIP_LIST_P            0.5

struct Node; // forward definition

struct Forward {
  struct Node *forward;
  int          span;
}

struct Node {
  SKIP_LIST_KEY_TYPE    key;
  SKIP_LIST_VALUE_TYPE  value;
  struct Forward        forwards[]; // flexible array member
};

struct SkipList {
  struct Node *head;
  int          level;
  int          length;
};

struct Node *CreateNode(int level) {
  struct Node *node;
  assert(level > 0);
  node = malloc(sizeof(struct Node) + sizeof(struct Forward) * level);
  return node;
}

struct SkipList *CreateSkipList() {
  struct SkipList *list;
  struct Node     *head;
  int              i;

  list = malloc(sizeof(struct SkipList));
  head = CreateNode(SKIP_LIST_MAX_LEVEL);
  for (i = 0; i < SKIP_LIST_MAX_LEVEL; i++) {
    head->forwards[i].forward = NULL;
    head->forwards[i].span = 0;
  }

  list->head = head;
  list->level = 1;

  return list;
}

接下來需要修改插入和刪除操作，來保證在跳躍表修改后跨度的數據完整性。

需要注意的是，在插入過程中需要使用 indices 記錄在每個層級遍歷到的最后一個元素的位置，這樣通過做簡單的減法操作就可以知道每個層級遍歷到的最后一個元素到新插入節點的跨度。

struct Node *SkipListInsert(struct SkipList *list, SKIP_LIST_KEY_TYPE key, SKIP_LIST_VALUE_TYPE value) {
  struct Node *update[SKIP_LIST_MAX_LEVEL];
  struct Node *current;
  int          indices[SKIP_LIST_MAX_LEVEL];
  int          i;
  int          level;

  current = list->head;
  for (i = list->level - 1; i >= 0; i--) {
    if (i == list->level - 1) {
      indices[i] = 0;
    } else {
      indices[i] = indices[i + 1];
    }
    
    while (current->forwards[i].forward && current->forwards[i].forward->key < target) {
      indices[i] += current->forwards[i].span;
      current = current->forwards[i].forward;
    }
    update[i] = current;
  }

  current = current->forwards[0].forward;
  if (current->key == target) {
    current->value = value;
    return current;
  }

  level = SkipListRandomLevel();
  if (level > list->level) {
    for (i = list->level; i < level; i++) {
      indices[i] = 0;
      update[i] = list->header;
      update[i]->forwards[i].span = list->length;
    }
  }

  current = CreateNode(level);
  current->key = key;
  current->value = value;

  for (i = 0; i < level; i++) {
    current->forwards[i].forward = update[i]->forwards[i].forward;
    update[i]->forwards[i].forward = current;
    current->forwards[i].span = update[i]->forwards[i].span - (indices[0] - indices[i]);
    update[i]->forwards[i].span = (indices[0] - indices[i]) + 1;
  }

  list.length++;

  return current;
}

struct Node *SkipListDelete(struct SkipList *list, SKIP_LIST_KEY_TYPE key) {
  struct Node *update[SKIP_LIST_MAX_LEVEL];
  struct Node *current;
  int          i;

  current = list->head;
  for (i = list->level - 1; i >= 0; i--) {
    while (current->forwards[i].forward && current->forwards[i].forward->key < key) {
      current = current->forwards[i].forward;
    }
    update[i] = current;
  }

  current = current->forwards[0].forward;
  if (current && current->key == key) {
    for (i = 0; i < list->level; i++) {
      if (update[i]->forwards[i].forward == current) {
        update[i]->forwards[i].forward = current->forwards[i];
        update[i]->forwards[i].span += current->forwards[i].span - 1;
      } else {
        break;
      }
    }

    while (list->level > 1 && list->head->forwards[list->level - 1] == NULL) {
      list->level--;
    }
  }

  return current;
}

當實現了快速隨機訪問之后，通過簡單的指針操作即可實現區間查詢功能。

審核編輯：湯梓紅