二、湊零錢問題

先看下題目：給你k種面值的硬幣，面值分別為c1, c2 ... ck，每種硬幣的數(shù)量無限，再給一個(gè)總金額amount，問你最少需要幾枚硬幣湊出這個(gè)金額，如果不可能湊出，算法返回 -1 。算法的函數(shù)簽名如下：

// coins 中是可選硬幣面值，amount 是目標(biāo)金額
int coinChange(int[] coins, int amount);

比如說k = 3，面值分別為 1，2，5，總金額amount = 11。那么最少需要 3 枚硬幣湊出，即 11 = 5 + 5 + 1。

你認(rèn)為計(jì)算機(jī)應(yīng)該如何解決這個(gè)問題？顯然，就是把所有肯能的湊硬幣方法都窮舉出來，然后找找看最少需要多少枚硬幣。

1、暴力遞歸

首先，這個(gè)問題是動(dòng)態(tài)規(guī)劃問題，因?yàn)樗哂小缸顑?yōu)子結(jié)構(gòu)」。 要符合「最優(yōu)子結(jié)構(gòu)」，子問題間必須互相獨(dú)立 。啥叫相互獨(dú)立？你肯定不想看數(shù)學(xué)證明，我用一個(gè)直觀的例子來講解。

比如說，你的原問題是考出最高的總成績(jī)，那么你的子問題就是要把語文考到最高，數(shù)學(xué)考到最高…… 為了每門課考到最高，你要把每門課相應(yīng)的選擇題分?jǐn)?shù)拿到最高，填空題分?jǐn)?shù)拿到最高…… 當(dāng)然，最終就是你每門課都是滿分，這就是最高的總成績(jī)。

得到了正確的結(jié)果：最高的總成績(jī)就是總分。因?yàn)檫@個(gè)過程符合最優(yōu)子結(jié)構(gòu)，“每門科目考到最高”這些子問題是互相獨(dú)立，互不干擾的。

但是，如果加一個(gè)條件：你的語文成績(jī)和數(shù)學(xué)成績(jī)會(huì)互相制約，此消彼長(zhǎng)。這樣的話，顯然你能考到的最高總成績(jī)就達(dá)不到總分了，按剛才那個(gè)思路就會(huì)得到錯(cuò)誤的結(jié)果。因?yàn)樽訂栴}并不獨(dú)立，語文數(shù)學(xué)成績(jī)無法同時(shí)最優(yōu)，所以最優(yōu)子結(jié)構(gòu)被破壞。

回到湊零錢問題，為什么說它符合最優(yōu)子結(jié)構(gòu)呢？比如你想求amount = 11時(shí)的最少硬幣數(shù)（原問題），如果你知道湊出amount = 10的最少硬幣數(shù)（子問題），你只需要把子問題的答案加一（再選一枚面值為 1 的硬幣）就是原問題的答案，因?yàn)橛矌诺臄?shù)量是沒有限制的，子問題之間沒有相互制，是互相獨(dú)立的。

那么，既然知道了這是個(gè)動(dòng)態(tài)規(guī)劃問題，就要思考 如何列出正確的狀態(tài)轉(zhuǎn)移方程 。

先確定「狀態(tài)」 ，也就是原問題和子問題中變化的變量。由于硬幣數(shù)量無限，所以唯一的狀態(tài)就是目標(biāo)金額amount。

然后確定dp函數(shù)的定義 ：函數(shù) dp(n)表示，當(dāng)前的目標(biāo)金額是n，至少需要dp(n)個(gè)硬幣湊出該金額。

然后確定「選擇」并擇優(yōu) ，也就是對(duì)于每個(gè)狀態(tài)，可以做出什么選擇改變當(dāng)前狀態(tài)。具體到這個(gè)問題，無論當(dāng)?shù)哪繕?biāo)金額是多少，選擇就是從面額列表coins中選擇一個(gè)硬幣，然后目標(biāo)金額就會(huì)減少：

# 偽碼框架
def coinChange(coins: List[int], amount: int):
    # 定義：要湊出金額 n，至少要 dp(n) 個(gè)硬幣
    def dp(n):
        # 做選擇，需要硬幣最少的那個(gè)結(jié)果就是答案
        for coin in coins:
            res = min(res, 1 + dp(n - coin))
        return res
    # 我們要求目標(biāo)金額是 amount
    return dp(amount)

最后明確 base case ，顯然目標(biāo)金額為 0 時(shí)，所需硬幣數(shù)量為 0；當(dāng)目標(biāo)金額小于 0 時(shí)，無解，返回 -1：

def coinChange(coins: List[int], amount: int):

    def dp(n):
        # base case
        if n == 0: return 0
        if n < 0: return -1
        # 求最小值，所以初始化為正無窮
        res = float('INF')
        for coin in coins:
            subproblem = dp(n - coin)
            # 子問題無解，跳過
            if subproblem == -1: continue
            res = min(res, 1 + subproblem)

        return res if res != float('INF') else -1

    return dp(amount)

至此，狀態(tài)轉(zhuǎn)移方程其實(shí)已經(jīng)完成了，以上算法已經(jīng)是暴力解法了，以上代碼的數(shù)學(xué)形式就是狀態(tài)轉(zhuǎn)移方程：

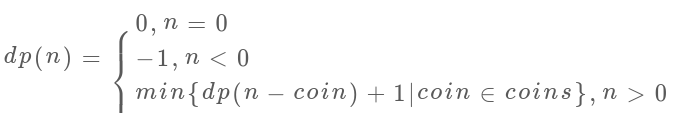
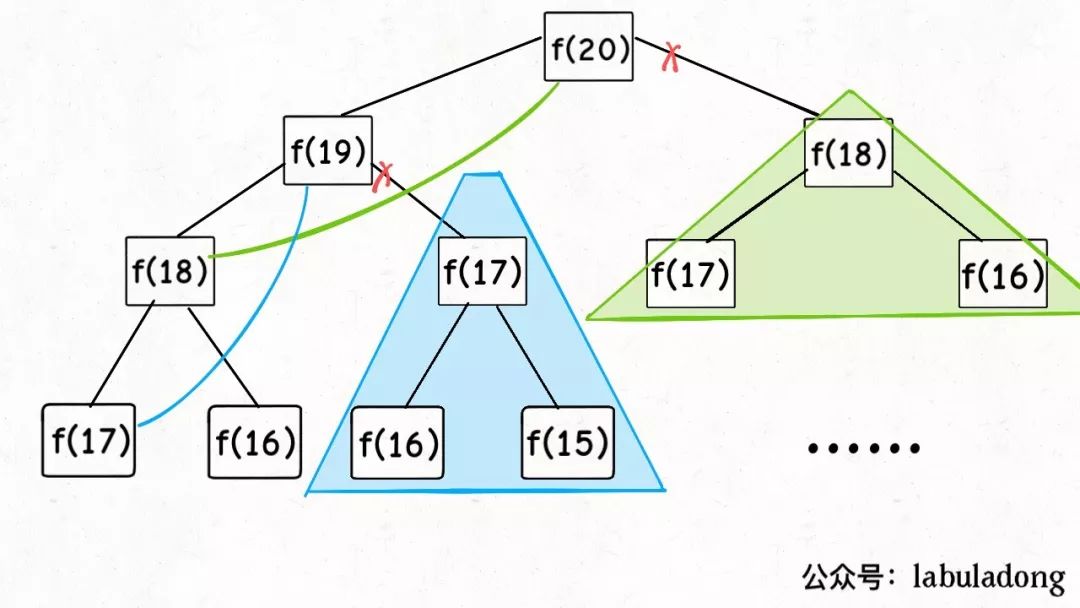
至此，這個(gè)問題其實(shí)就解決了，只不過需要消除一下重疊子問題，比如amount = 11, coins = {1,2,5}時(shí)畫出遞歸樹看看：

時(shí)間復(fù)雜度分析：子問題總數(shù) x 解決每個(gè)子問題的時(shí)間 。

子問題總數(shù)為遞歸樹節(jié)點(diǎn)個(gè)數(shù)，這個(gè)比較難看出來，是 O(n^k)，總之是指數(shù)級(jí)別的。每個(gè)子問題中含有一個(gè) for 循環(huán)，復(fù)雜度為 O(k)。所以總時(shí)間復(fù)雜度為 O(k * n^k)，指數(shù)級(jí)別。

2、帶備忘錄的遞歸

只需要稍加修改，就可以通過備忘錄消除子問題：

def coinChange(coins: List[int], amount: int):
    # 備忘錄
    memo = dict()
    def dp(n):
        # 查備忘錄，避免重復(fù)計(jì)算
        if n in memo: return memo[n]

        if n == 0: return 0
        if n < 0: return -1
        res = float('INF')
        for coin in coins:
            subproblem = dp(n - coin)
            if subproblem == -1: continue
            res = min(res, 1 + subproblem)

        # 記入備忘錄
        memo[n] = res if res != float('INF') else -1
        return memo[n]

    return dp(amount)

不畫圖了，很顯然「?jìng)渫洝勾蟠鬁p小了子問題數(shù)目，完全消除了子問題的冗余，所以子問題總數(shù)不會(huì)超過金額數(shù) n，即子問題數(shù)目為 O(n)。處理一個(gè)子問題的時(shí)間不變，仍是 O(k)，所以總的時(shí)間復(fù)雜度是 O(kn)。

3、dp 數(shù)組的迭代解法

當(dāng)然，我們也可以自底向上使用 dp table 來消除重疊子問題，dp數(shù)組的定義和剛才dp函數(shù)類似，定義也是一樣的：

dp[i] = x表示，當(dāng)目標(biāo)金額為i時(shí)，至少需要x枚硬幣 。

int coinChange(vector<int>& coins, int amount) {
    // 數(shù)組大小為 amount + 1，初始值也為 amount + 1
    vector<int> dp(amount + 1, amount + 1);
    // base case
    dp[0] = 0;
    for (int i = 0; i < dp.size(); i++) {
        // 內(nèi)層 for 在求所有子問題 + 1 的最小值
        for (int coin : coins) {
            // 子問題無解，跳過
            if (i - coin < 0) continue;
            dp[i] = min(dp[i], 1 + dp[i - coin]);
        }
    }
    return (dp[amount] == amount + 1) ? -1 : dp[amount];
}

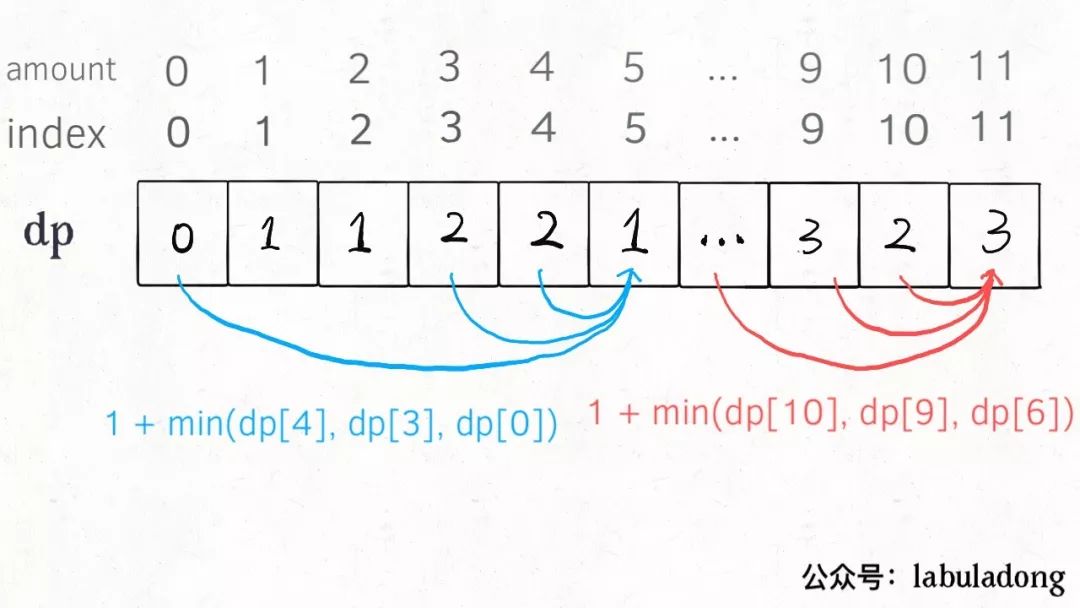
PS：為啥dp數(shù)組初始化為amount + 1呢，因?yàn)闇惓?code>amount金額的硬幣數(shù)最多只可能等于amount（全用 1 元面值的硬幣），所以初始化為amount + 1就相當(dāng)于初始化為正無窮，便于后續(xù)取最小值。

三、最后總結(jié)

第一個(gè)斐波那契數(shù)列的問題，解釋了如何通過「?jìng)渫洝够蛘摺竏p table」的方法來優(yōu)化遞歸樹，并且明確了這兩種方法本質(zhì)上是一樣的，只是自頂向下和自底向上的不同而已。

第二個(gè)湊零錢的問題，展示了如何流程化確定「狀態(tài)轉(zhuǎn)移方程」，只要通過狀態(tài)轉(zhuǎn)移方程寫出暴力遞歸解，剩下的也就是優(yōu)化遞歸樹，消除重疊子問題而已。

如果你不太了解動(dòng)態(tài)規(guī)劃，還能看到這里，真得給你鼓掌，相信你已經(jīng)掌握了這個(gè)算法的設(shè)計(jì)技巧。

計(jì)算機(jī)解決問題其實(shí)沒有任何奇技淫巧，它唯一的解決辦法就是窮舉 ，窮舉所有可能性。算法設(shè)計(jì)無非就是先思考“如何窮舉”，然后再追求“如何聰明地窮舉”。

列出動(dòng)態(tài)轉(zhuǎn)移方程，就是在解決“如何窮舉”的問題。之所以說它難，一是因?yàn)楹芏喔F舉需要遞歸實(shí)現(xiàn)，二是因?yàn)橛械膯栴}本身的解空間復(fù)雜，不那么容易窮舉完整。

備忘錄、DP table 就是在追求“如何聰明地窮舉”。用空間換時(shí)間的思路，是降低時(shí)間復(fù)雜度的不二法門，除此之外，試問，還能玩出啥花活？