傅里葉變換是將按時(shí)間或空間采樣的信號與按頻率采樣的相同信號進(jìn)行關(guān)聯(lián)的數(shù)學(xué)公式。在信號處理中，傅里葉變換可以揭示信號的重要特征（即其頻率分量）。

對于包含 n 個(gè)均勻采樣點(diǎn)的向量 x，其傅里葉變換定義為

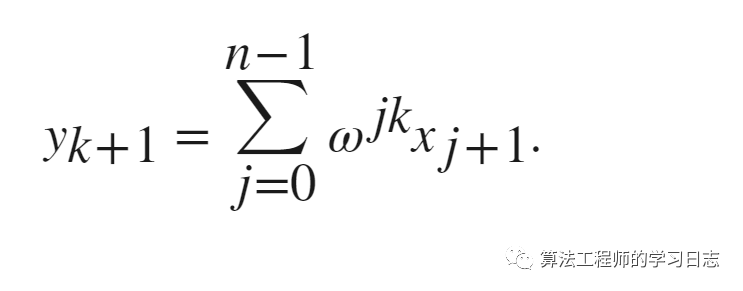
ω=e?2πi/n 是 n 個(gè)復(fù)單位根之一，其中 i 是虛數(shù)單位。對于 x 和 y，索引 j 和 k 的范圍為 0 到 n?1。

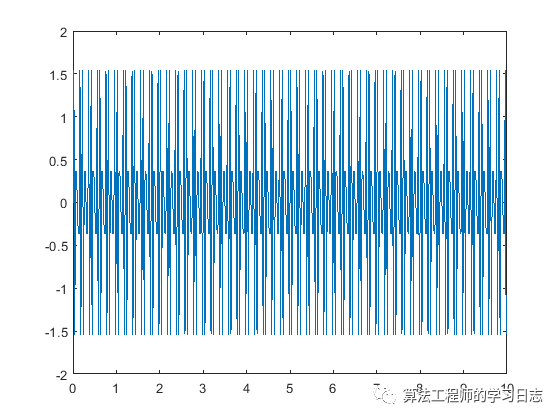
MATLAB中的 fft 函數(shù)使用快速傅里葉變換算法來計(jì)算數(shù)據(jù)的傅里葉變換。以正弦信號 x 為例，該信號是時(shí)間 t 的函數(shù)，頻率分量為 15 Hz 和 20 Hz。使用在 10 秒周期內(nèi)以 150 秒為增量進(jìn)行采樣的時(shí)間向量。

t = 0:1/50:10-1/50;                     
x = sin(2*pi*15*t) + sin(2*pi*20*t);
figure
plot(t,x)

計(jì)算信號的傅里葉變換，并在頻率空間創(chuàng)建對應(yīng)于信號采樣的向量 f。

y = fft(x);     
f = (0:length(y)-1)*50/length(y);

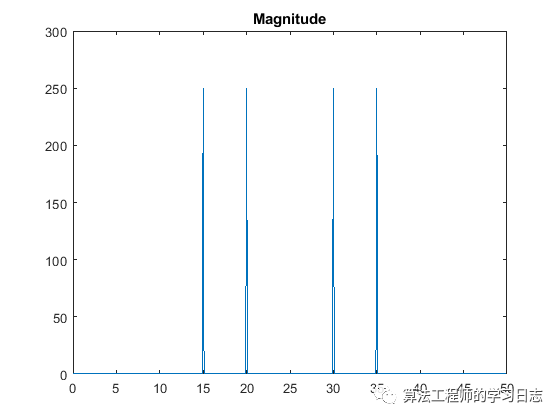
以頻率函數(shù)形式繪制信號幅值時(shí)，幅值尖峰對應(yīng)于信號的 15 Hz 和 20 Hz 頻率分量。

figure
plot(f,abs(y))
title('Magnitude')

該變換還會(huì)生成尖峰的鏡像，對應(yīng)于信號的負(fù)頻率。為了更好地以可視化方式呈現(xiàn)周期性，使用 fftshift 函數(shù)對變換執(zhí)行以零為中心的循環(huán)平移。

n = length(x);                         
fshift = (-n/2:n/2-1)*(50/n);
yshift = fftshift(y);
figure
plot(fshift,abs(yshift))

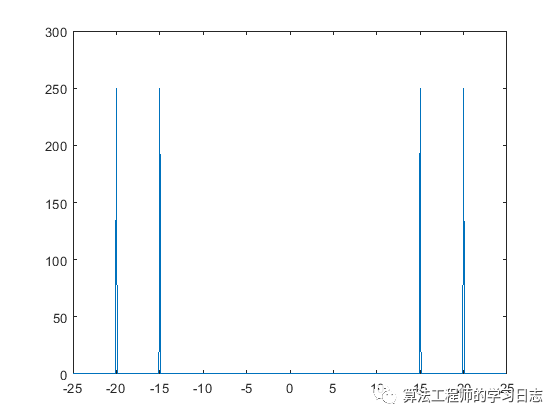
含噪信號

在科學(xué)應(yīng)用中，信號經(jīng)常遭到隨機(jī)噪聲破壞，掩蓋其頻率分量。傅里葉變換可以清除隨機(jī)噪聲并顯現(xiàn)頻率。例如，通過在原始信號 x 中注入高斯噪聲，創(chuàng)建一個(gè)新信號 xnoise。

rng('default')
xnoise = x + 2.5*randn(size(t));

頻率函數(shù)形式的信號功率是信號處理中的一種常用度量。功率是信號的傅里葉變換按頻率樣本數(shù)進(jìn)行歸一化后的平方幅值。計(jì)算并繪制以零頻率為中心的含噪信號的功率譜。盡管存在噪聲，仍可以根據(jù)功率中的尖峰辨識出信號的頻率。

ynoise = fft(xnoise);
ynoiseshift = fftshift(ynoise);    
power = abs(ynoiseshift).^2/n; 
figure
plot(fshift,power)
title('Power')

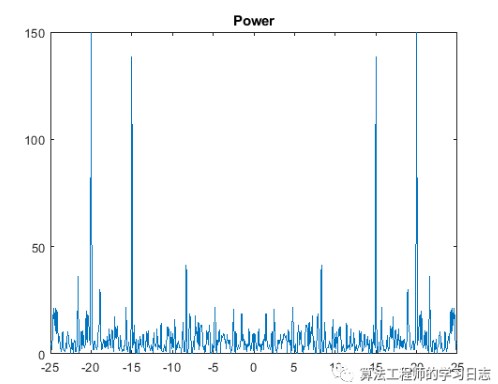
計(jì)算效率

直接使用傅里葉變換公式分別計(jì)算 y 的 n 個(gè)元素需要 n平方 數(shù)量級的浮點(diǎn)運(yùn)算。使用快速傅里葉變換算法，則只需要 nlogn 數(shù)量級的運(yùn)算。在處理包含成百上千萬個(gè)數(shù)據(jù)點(diǎn)的數(shù)據(jù)時(shí)，這一計(jì)算效率會(huì)帶來很大的優(yōu)勢。在 n 為 2 的冪時(shí)，許多專門的快速傅里葉變換實(shí)現(xiàn)可進(jìn)一步提高效率。

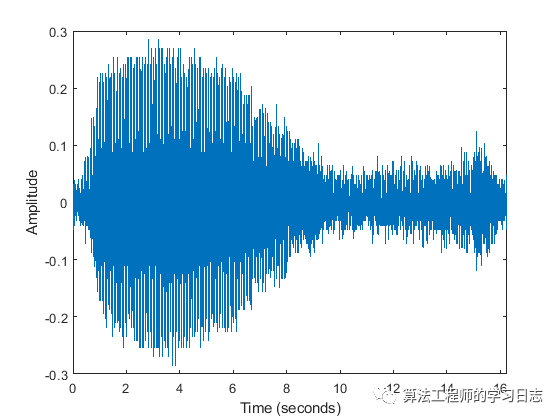
以加利福尼亞海岸的水下麥克風(fēng)所收集的音頻數(shù)據(jù)為例。在康奈爾大學(xué)生物聲學(xué)研究項(xiàng)目維護(hù)的庫中可以找到這些數(shù)據(jù)。載入包含太平洋藍(lán)鯨鳴聲的文件 bluewhale.au，并對其中一部分?jǐn)?shù)據(jù)進(jìn)行格式化。可使用命令 sound(x,fs) 來收聽完整的音頻文件。

whaleFile = 'bluewhale.au';
[x,fs] = audioread(whaleFile);
whaleMoan = x(2.45e4:3.10e4);
t = 10*(0:1/fs:(length(whaleMoan)-1)/fs);
figure
plot(t,whaleMoan)
xlabel('Time (seconds)')
ylabel('Amplitude')
xlim([0 t(end)])

指定新的信號長度，該長度是大于原始長度的最鄰近的 2 的冪。然后使用 fft 和新的信號長度計(jì)算傅里葉變換。fft 會(huì)自動(dòng)用零填充數(shù)據(jù)，以增加樣本大小。此填充操作可以大幅提高變換計(jì)算的速度，對于具有較大質(zhì)因數(shù)的樣本大小更是如此。

m = length(whaleMoan); 
n = pow2(nextpow2(m));
y = fft(whaleMoan,n);

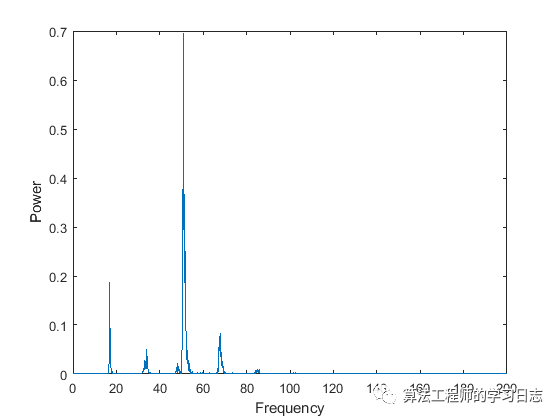
繪制信號的功率譜。繪圖指示，鳴聲包含約 17 Hz 的基本頻率和一系列諧波（其中強(qiáng)調(diào)了第二個(gè)諧波）。

f = (0:n-1)*(fs/n)/10; % frequency vector
power = abs(y).^2/n;   % power spectrum      
figure
plot(f(1:floor(n/2)),power(1:floor(n/2)))
xlabel('Frequency')
ylabel('Power')