光學(xué)系統(tǒng)多用于對物體成像。未經(jīng)嚴(yán)格設(shè)計的光學(xué)系統(tǒng)只有在近軸區(qū)才能成完善像。由于在近軸區(qū)成像的范圍和光束寬度均趨于無限小,因此沒有很大的實用意義。
實際的光學(xué)系統(tǒng)要求對一定大小的物體、以一定寬度的光束成近似完善的像。
“應(yīng)用光學(xué)”所要解決的問題就是尋求這樣的光學(xué)系統(tǒng)。
為了估計和比較實際光學(xué)系統(tǒng)成像質(zhì)量是否符合完善成像條件,需要建立一個模型,使之滿足物空間的同心光束經(jīng)系統(tǒng)后仍為同心光束,或者說,物空間一點通過系統(tǒng)成像后仍為一點。這個模型稱為理想光學(xué)系統(tǒng),它對任意大的物體、以任意寬的光束成像都是完善的。
在均勻透明的介質(zhì)中,除平面反射鏡具有上述理想光學(xué)系統(tǒng)的性質(zhì)外,任何實際的光學(xué)系統(tǒng)都不能絕對完善地成像。
理想光學(xué)系統(tǒng)理論是在1841年由高斯提出來的。1893年阿貝發(fā)展了理想光學(xué)系統(tǒng)的理論。理想光學(xué)系統(tǒng)理論又稱為“高斯光學(xué)”,因為在計算理想光學(xué)系統(tǒng)各個參量之間的關(guān)系常為階線性方程,也稱為“一階光學(xué)”。
理想光學(xué)系統(tǒng)處于各向同性的均勻介質(zhì)中,物空間中的光線和像空間中的光線均為直線。在物空間的一點,對應(yīng)于像空間的一點,這樣的一對點的位置是用光線通過一定的幾何關(guān)系確定下來的,因而把這種幾何關(guān)系稱為“共線成像”、“共線變換”或“共線光學(xué)”。這種“共線成像”理論的初始幾何定義可歸結(jié)為
(1)物像空間的共軛點物空間中每一點對應(yīng)于像空間中的相應(yīng)的點,且只對應(yīng)一個點。這兩個對應(yīng)點稱為物像空間的共軛點。
(2)物像空間的共軛線物空間中的每一條直線對應(yīng)于像空間的相應(yīng)的直線,而且只對應(yīng)一條。這兩條對應(yīng)直線稱為物像空間的共軛線。
(3)共線成像關(guān)系物空間的任意一點位于一條直線上,那么在像空間內(nèi)的共軛點必在該直線的共軛線上。
由以上定義可以推出:物空間中任一平面對應(yīng)于像空間中有一共軛平面。物空間中每一同心光束在像空間中均有一共軛同心光束與之相對應(yīng)。
“共線成像”理論是理想光學(xué)系統(tǒng)的理論基礎(chǔ)。一般來說,這種共線成像并不一定能滿足像與物的相似。為了使像和物在幾何形狀上完全相似,總是取物平面垂直于光學(xué)系統(tǒng)的光軸在實際光學(xué)系統(tǒng)的近軸區(qū)可以滿足共線成像理論。因此,在進(jìn)行光學(xué)系統(tǒng)設(shè)計時,往往以其近軸區(qū)成像性質(zhì)來衡量該系統(tǒng)的成像質(zhì)量。
理想光學(xué)系統(tǒng)只作為光學(xué)系統(tǒng)的一個理論模型,它不涉及到光學(xué)系統(tǒng)的具體結(jié)構(gòu)r、d和n,對于理想光學(xué)系統(tǒng)的討論是根據(jù)共線成像理論來研究物和像之間的關(guān)系。
首先來研究理想光學(xué)系統(tǒng)的一些特定的點和面,它們往往可以完全表示該系統(tǒng)的特性。
1. 焦點與焦平面
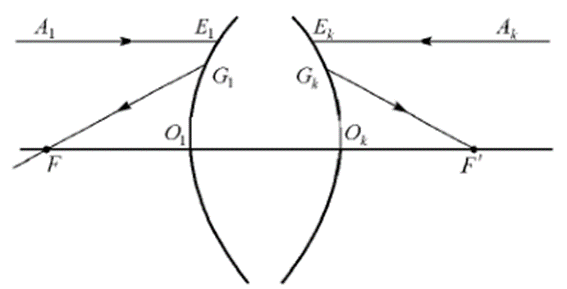
圖1:焦點與焦平面
根據(jù)理想光學(xué)系統(tǒng)共線成像的特性,設(shè)在物空間有一條和光學(xué)系統(tǒng)光軸平行的光線射入到光學(xué)系統(tǒng),則在像空間必有一條光線與之相共軛。
隨著光學(xué)系統(tǒng)性質(zhì)的不同,共軛光線可以平行于光軸也可以和光軸交于點。首先研究后一種情況。如圖1所示,O1和Ok為理想光學(xué)系統(tǒng)的第一個面和最后一個面,F(xiàn)O1OkF`是光軸,平行于光軸的光線A1E1經(jīng)過光學(xué)系統(tǒng)各面折射后,沿GkF`方向射出,交光軸于F`點。沿光軸入射的光線FO1沒有折射地通過系統(tǒng)仍沿光軸射出。由于像方的出射光線GkF`和OkF`分別和物方的入射光線A1E1和FO1相共軛,因此光線GkF`和OkF`的交點F`的共軛點應(yīng)該是光線AE和FO1的交點,顯然它位于左方無限遠(yuǎn)的光軸上,所以F`是物方無限遠(yuǎn)軸上點的像。所有其他平行于光軸入射的光線均應(yīng)會聚于點F`,點F`稱為光學(xué)系統(tǒng)的像方焦點(后焦點或第二焦點)。
如果從像方無限遠(yuǎn)處射入一束與光學(xué)系統(tǒng)光軸平行的光束,同樣會聚在物方光軸上一點F,稱為光學(xué)系統(tǒng)的物方焦點(前焦點或第一焦點),其與像方無限遠(yuǎn)處光軸上點相共軛。
但應(yīng)指出,物方焦點F和像方焦點F`不是一對共軛點。
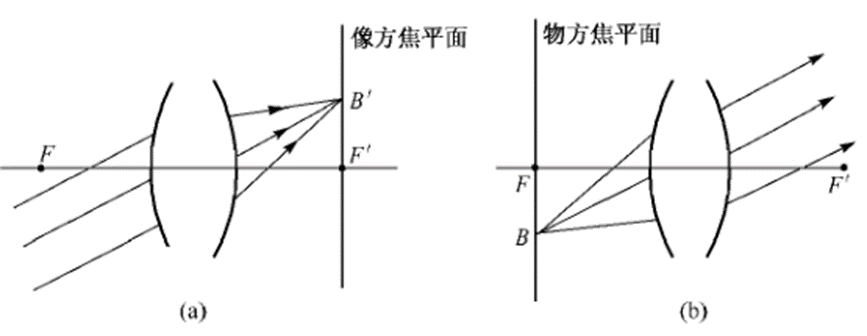
圖2:光學(xué)系統(tǒng)的焦平面示意圖
經(jīng)過像方焦點F`作一垂軸平面稱為像方焦平面,顯然這是物方無限遠(yuǎn)處垂軸平面的共軛面。由物方無限遠(yuǎn)處射來的任何方向的平行光束,經(jīng)光學(xué)系統(tǒng)后必會聚于像方焦平面上一點B’,如圖2(a)所示。通過物方焦點F的垂軸平面稱為物方焦平面,它和像方無限遠(yuǎn)處的垂軸平面相共軛。自物方焦平面上任一點發(fā)出的光束經(jīng)光學(xué)系統(tǒng)以后,均以平行光射出,如圖2(b)所示。
2. 主點與主平面
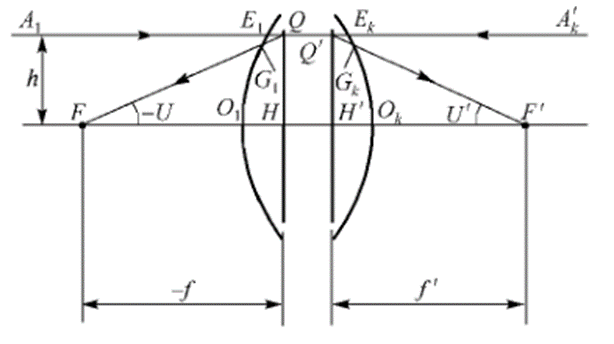
圖3:主點與主平面
在圖3中,延長入射光線A1E1與出射光線GkF`得到交點Q`。同樣,在像空間延長光線A`kEk與其在物空間的共軛光線G1F交于點Q,如圖3所示。設(shè)光線A1E1和光線A`kEk的入射高度相同,且都在子午面內(nèi)。
顯然,點Q和點Q`是一對共軛點。點Q是光線A1E1和FQ交成的“虛物點”,而Q`是光線A1E1和FQ的共軛光線A`kEk和F`Q`交成的“虛像點”。過點Q和Q`作與光軸垂直的平面QH和Q`H`。顯然,這對平面是互相共軛的。在這對平面內(nèi)的任意共軛線段如QH和Q`H`具有同樣的高度,而且在光軸的同一側(cè),故其放大率為+1。稱這對放大率為+1的共軛平面為主平面,QH稱為物方主平面(前主面或第一主面),Q`H`稱為像方主平面(后主面或第二主平面)。
除入射為平行光束、出射也是平行光束的望遠(yuǎn)系統(tǒng)外,所有光學(xué)系統(tǒng)都有一對主面,其一個主面上的任一段以相等的大小和相同的方向成像在另一個主面上。
主平面與光軸的交點H和H`稱為主點。H為物方主點(前主點或第一主點),H`為像方主點(后主點和第二主點),兩個主點是相共軛的。
3. 焦距
自光學(xué)系統(tǒng)的物方主點H到物方焦點F的距離稱為物方焦距(前焦距或第一焦距),用字母f表示。同樣,像方主點H'到像方焦點F'的距離稱為像方焦距(后焦距或第二焦距),用字母f`表示。焦距值的正、負(fù)是以相應(yīng)的主點為原點來確定的,如果由主點到相應(yīng)焦點的方向與光線的傳播方向一致,則焦距為正,反之為負(fù)。在圖3中,f<0,f`>0。如果平行于光軸的入射光線的入射高度為h,其共軛光線與光軸的交角為U`,則由三角形Q`H`F`可以得到像方焦距的表示式為
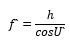
同理,可以得出物方焦距的表示式為
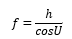
對于理想光學(xué)系統(tǒng),不管其結(jié)構(gòu)(r、d、n)如何,只要知道其焦距值和焦點或主點的位置,其性質(zhì)就確定了,同時可以方便地用作圖或解析的方法求得任意位置和大小的物體經(jīng)光學(xué)系統(tǒng)所成的角。
4. 理想光學(xué)系統(tǒng)的二焦距間關(guān)系
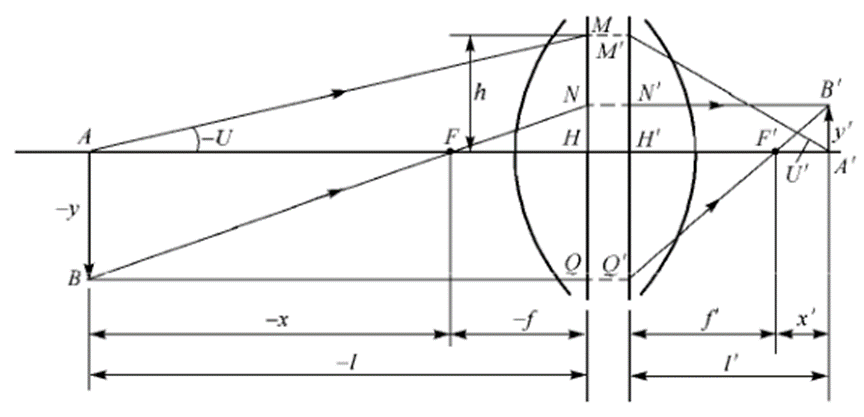
圖4:光學(xué)系統(tǒng)焦距間的關(guān)系
在圖4中,軸上物點A發(fā)出的光線AM與光軸交角為U,交物方主面于點M,入射高度為h,AM的共軛光線M`A`交像方主面于點M',與光軸交角為U`,由直角三角形AMH和A`M`H`,得
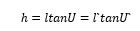
或
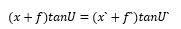
由于三角形ABF與三角形FNH相似、三角形A`B`F`與三角形Q`H`F`相似,因此可得
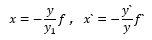
將其代入上式中,得
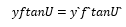
對于理想光學(xué)系統(tǒng),不論U和U`多大、y和y`多大,上式總能成立。當(dāng)然,對于小孔徑、小視場的近軸區(qū),上式也成立,只是用弧度取代角度的正切,得

與拉赫不變量nuy=n`u`y`相比較,可以得出表征光學(xué)系統(tǒng)物方和像方焦距之間關(guān)系的重要公式:
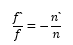
即光學(xué)系統(tǒng)像方焦距f`物方焦距f之比等于相應(yīng)空間折射率之比的負(fù)值。
若光學(xué)系統(tǒng)在同一介質(zhì)中,即n`=n,則兩個焦距的絕對值相等、符號相反:

必須指出,若光學(xué)系統(tǒng)中包括反射面,則兩個焦距之間的關(guān)系由反射面的個數(shù)決定。
設(shè)反射面的數(shù)目為k,則可以寫成如下更一般的形式:
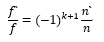
當(dāng)n`=n時,
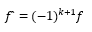
可知折射系統(tǒng)以及具有偶數(shù)個反射面的折、反射系統(tǒng),物方焦距和像方焦距異號。當(dāng)有奇數(shù)個反射面時,物方焦距和像方焦距同號。
5. 光學(xué)系統(tǒng)的節(jié)點
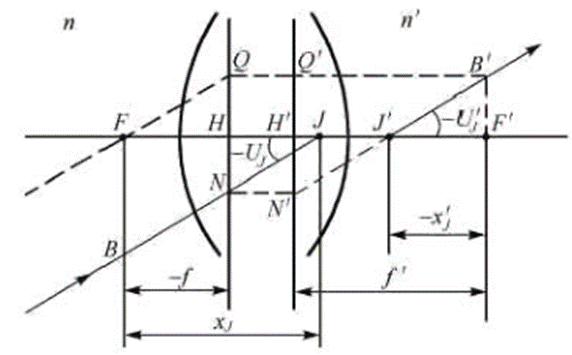
圖5:光學(xué)系統(tǒng)的節(jié)點的示意圖
在光學(xué)系統(tǒng)中還有一對角放大率為+1的共軛點J和J`。通過這對共軛點的光線方向不變,如圖5所示。三角形FQH與三角形J`B`F`全等,則FH=J`F`;三角形HNJ與三角形H`N`J`全等,則HJ=H`J`。又由圖5可知,xJ=HJ+FH=H`J`+ J`F`,x`J=J`F`=FH,即得以焦點為原點的節(jié)點的坐標(biāo):
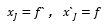
這一對共軛點分別稱為物方節(jié)點和像方節(jié)點,即以字母J和J`表示。
如果光學(xué)系統(tǒng)f<0,f>0,則節(jié)點位置坐標(biāo)為xJ=f`>0,x`J=f`<0,即節(jié)點J位于焦點F之
右|f`|處,J`位于焦點F`之左|f`|處。
過節(jié)點的共軛光線角放大率為+1,即UJ=U`J。若光學(xué)系統(tǒng)在同一介質(zhì)中,則有,f=-f`,則xJ=xH,x`J=x`H,即節(jié)點與主點重合。
主點、節(jié)點和焦點統(tǒng)稱為理想光學(xué)系統(tǒng)的基點。這些點的位置確定以后,理想光學(xué)系統(tǒng)的成像性質(zhì)就確定了。所以,光學(xué)系統(tǒng)的基點表征了理想光學(xué)系統(tǒng)的特性。
來源:小小光學(xué)08
審核編輯:湯梓紅
-
模型
+關(guān)注
關(guān)注
1文章
3516瀏覽量
50361 -
光學(xué)系統(tǒng)
+關(guān)注
關(guān)注
5文章
251瀏覽量
18728 -
光線
+關(guān)注
關(guān)注
0文章
73瀏覽量
10737
原文標(biāo)題:理想的光學(xué)系統(tǒng)
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
切換變倍光學(xué)系統(tǒng)設(shè)計
OCAD光學(xué)系統(tǒng)自動設(shè)計程序
光學(xué)自動設(shè)計及光學(xué)系統(tǒng)的分析
光線傳播的基本定律及幾何光學(xué)和光學(xué)設(shè)計等知識詳述
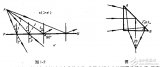
光學(xué)成像系統(tǒng)的原理
高斯光學(xué),理想的光學(xué)系統(tǒng)
光學(xué)系統(tǒng)低誤差敏感度設(shè)計方法的研究現(xiàn)狀與進(jìn)展
光學(xué)系統(tǒng)設(shè)計流程
光學(xué)系統(tǒng)的基本特性
光學(xué)系統(tǒng)設(shè)計的不可忽略的參數(shù)介紹
折反式變形光學(xué)系統(tǒng)設(shè)計
基于離軸成像光學(xué)系統(tǒng)的設(shè)計
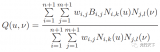
光學(xué)系統(tǒng)設(shè)計過程
光學(xué)系統(tǒng)的像方基本參數(shù)結(jié)構(gòu)示意圖
離軸光學(xué)系統(tǒng)的優(yōu)勢





 理想光學(xué)系統(tǒng)的研究
理想光學(xué)系統(tǒng)的研究











評論