這次的文章,我們來看一看三維空間直角坐標系的平移和旋轉(zhuǎn)變換,盡管這個內(nèi)容早已見諸文獻資料,但自己在看書籍以及期刊論文時,總是遇到讓人百思不得其解的事情,就是不同的文獻給出的同類型的旋轉(zhuǎn)矩陣居然有不一樣的,這讓小D對文獻中的公式產(chǎn)生了懷疑,也不知道哪個旋轉(zhuǎn)矩陣才是對的。
于是,自己動手,豐衣足食,為了驗證公式的正確性,小D把旋轉(zhuǎn)矩陣推了個遍,包括文獻中只給出了公式而沒有過程的旋轉(zhuǎn)矩陣的推導。
三維空間直角坐標系的平移變換
文章的開頭,還是先講講坐標系的平移變換,平移變換的過程如下圖所示:
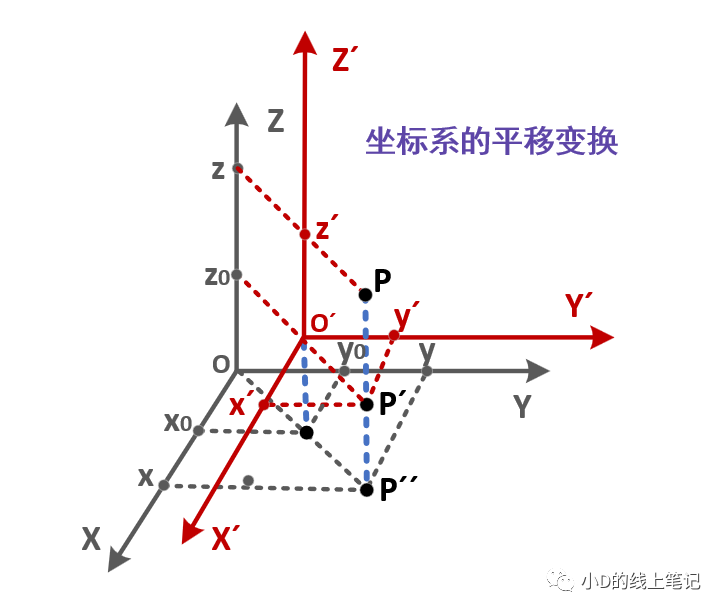
假設(shè)點P是空間中的任意一點,其在XYZ坐標系中的坐標為(x, y, z)。現(xiàn)在點P不動,我們將XYZ坐標系做一個平移的操作,把XYZ平移到X′Y′Z′的位置,O′是平移后的坐標的原點,要注意的是,O′在XYZ中的坐標為(x0, y0, z0)。點P在XYZ坐標系中的坐標為(x, y, z),點P在平移后的坐標系X′Y′Z′中的坐標為(x′, y′, z′)。根據(jù)上面這個示意圖,聰明的你一下就可以發(fā)現(xiàn):
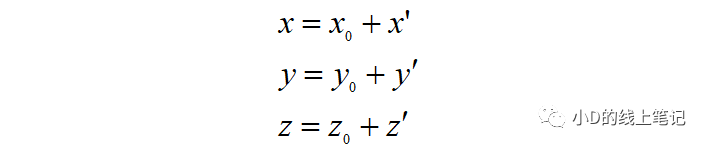
通過上面的式子,我們可以求解出點P在X′Y′Z′坐標系中的坐標為:
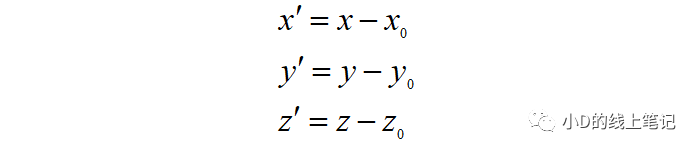
把上面的式子轉(zhuǎn)換成矩陣的形式就是:
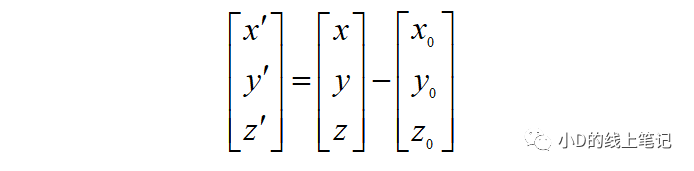
這就是三維空間直角坐標系的平移變換了。
三維空間直角坐標系的旋轉(zhuǎn)變換
下面我們來看看三維空間直角坐標系的旋轉(zhuǎn)變換,小D最開始在研究旋轉(zhuǎn)變換的時候,只推導了右手坐標系的旋轉(zhuǎn)變換。有一次看到了一篇文獻,它用的是左手坐標系,但小D對文獻中給出的公式的正確性感到懷疑,而我們要在代碼中用到相關(guān)的坐標轉(zhuǎn)換,這意味著我們需要知道左手坐標系旋轉(zhuǎn)矩陣的正確表達式,所以小D又把左手坐標系的旋轉(zhuǎn)矩陣推導了一遍。
右手坐標系的旋轉(zhuǎn)變換
右手坐標系的旋轉(zhuǎn)過程有三個,分別是繞X,Y,Z軸旋轉(zhuǎn),右手坐標系在旋轉(zhuǎn)時,通常規(guī)定以逆時針旋轉(zhuǎn)方向為正方向。
①XYZ右手坐標系繞X軸逆時針旋轉(zhuǎn)θ角
先來推導右手坐標系繞X軸旋轉(zhuǎn)的旋轉(zhuǎn)矩陣,這個過程可以用下面這個示意圖表示:
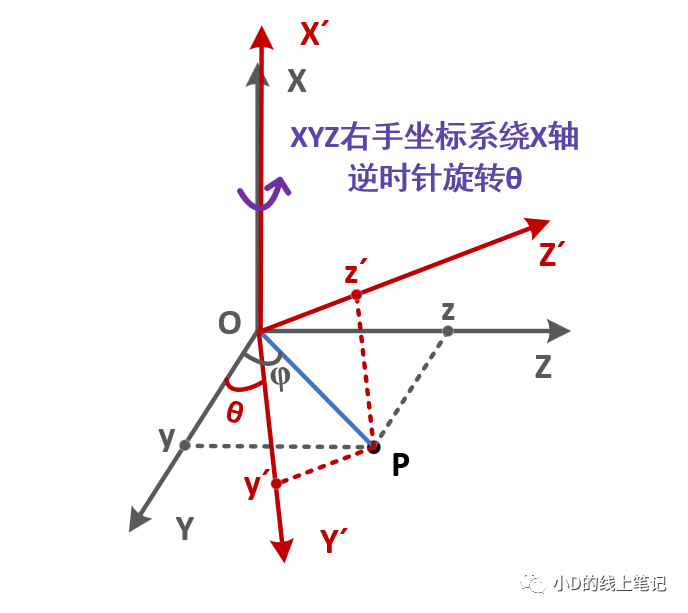
假設(shè)P點為空間中任意一點,為了便于觀察與推導,我們將P點放在YOZ平面內(nèi)。P點在空間中保持不動,XYZ坐標系繞X軸逆時針旋轉(zhuǎn)θ形成新的坐標系X′Y′Z′,P點在XYZ中的坐標為(x, y, z),P點在X′Y′Z′中的坐標為(x′, y′, z′),現(xiàn)在我們已知(x, y, z)、旋轉(zhuǎn)角度θ和(x′, y′, z′),求旋轉(zhuǎn)矩陣Rx。在推導的過程中,我們還要假設(shè)一個變量,就是點P相對于Y軸正方向逆時針的夾角為φ。
很明顯,點P在XYZ坐標系中的Y,Z軸坐標可以表示為:
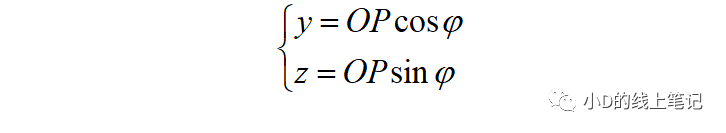
點P在X′Y′Z′坐標系中Y′,Z′軸坐標為:
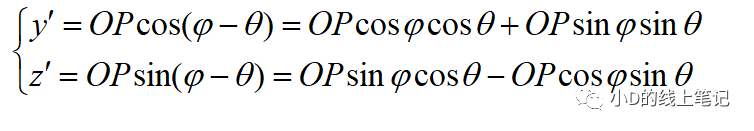
把x,y帶入x′,y′中,同時P點在XYZ中X軸坐標與其在X′Y′Z′坐標系中的X′軸坐標是相等的,所以有:
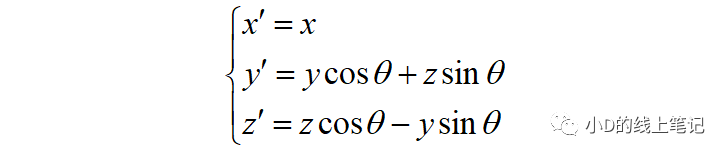
把這個表達式表示成矩陣相乘的形式為:
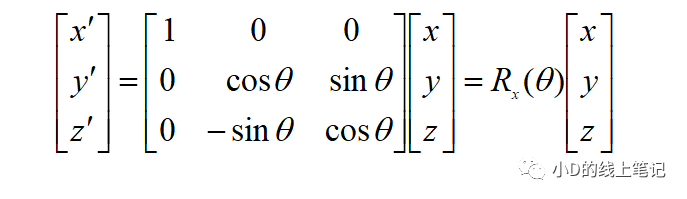
上面的Rx就是XYZ右手坐標系繞X軸逆時針旋轉(zhuǎn)θ角,空間中的點從XYZ坐標系變換到X′Y′Z′坐標系的旋轉(zhuǎn)矩陣,Rx的表達式為:
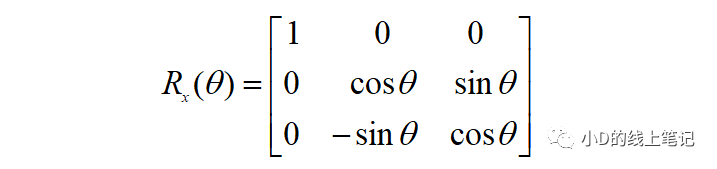
②XYZ右手坐標系繞Y軸逆時針旋轉(zhuǎn)θ角
有了前面的推導過程,XYZ右手坐標系繞Y軸逆時針旋轉(zhuǎn)θ角的旋轉(zhuǎn)矩陣的推導就一葫蘆畫瓢了。旋轉(zhuǎn)過程如下圖所示:
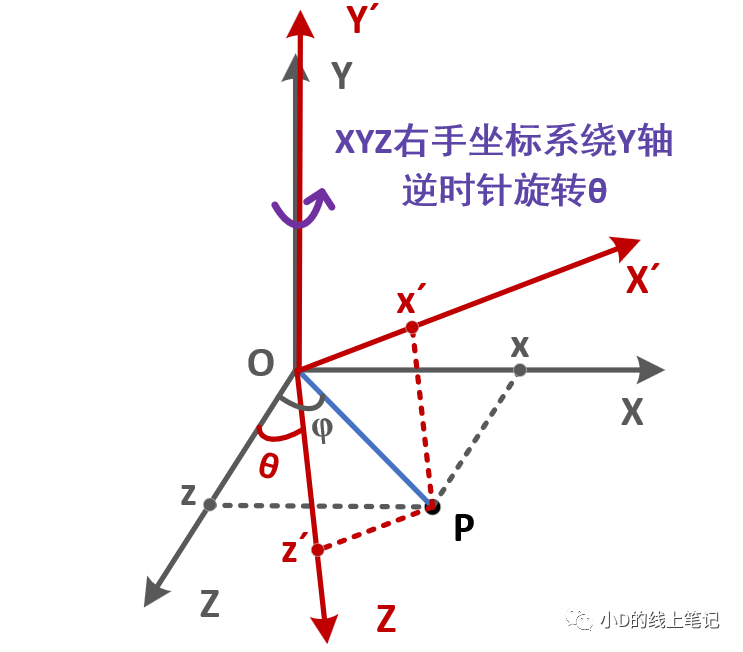
點P在XYZ右手坐標系中的X,Z軸坐標為:
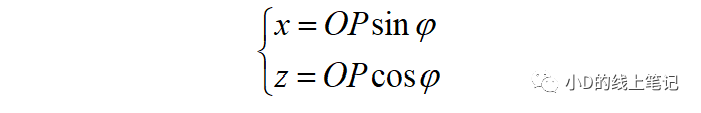
點P在X′Y′Z′坐標系中的X,Z軸坐標為:
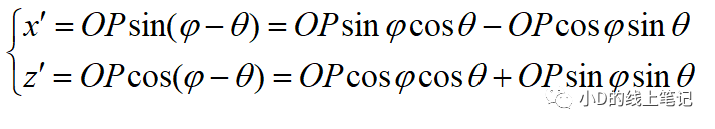
把x,z帶入x′,z′中,同時P點在XYZ中的Y軸坐標與X′Y′Z′坐標系中的Y′軸坐標是相等的,所以有:
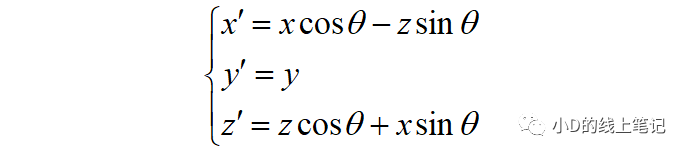
寫成矩陣相乘的形式:
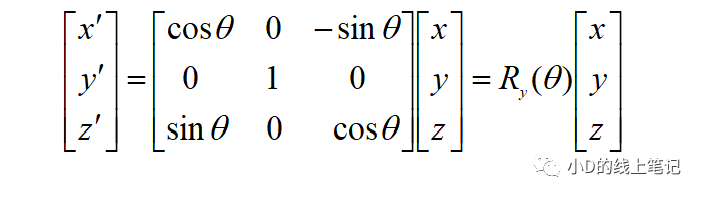
所以,XYZ右手坐標系繞Y軸逆時針旋轉(zhuǎn)θ角的旋轉(zhuǎn)矩陣Ry為:
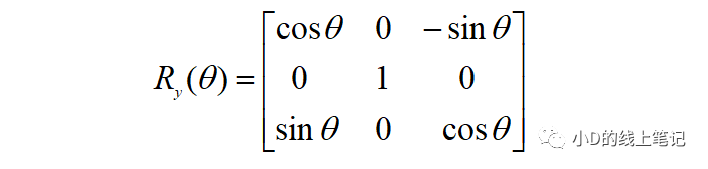
③XYZ右手坐標系繞Z軸逆時針旋轉(zhuǎn)θ角
XYZ右手坐標系繞Z軸逆時針旋轉(zhuǎn)θ的過程如下圖所示:
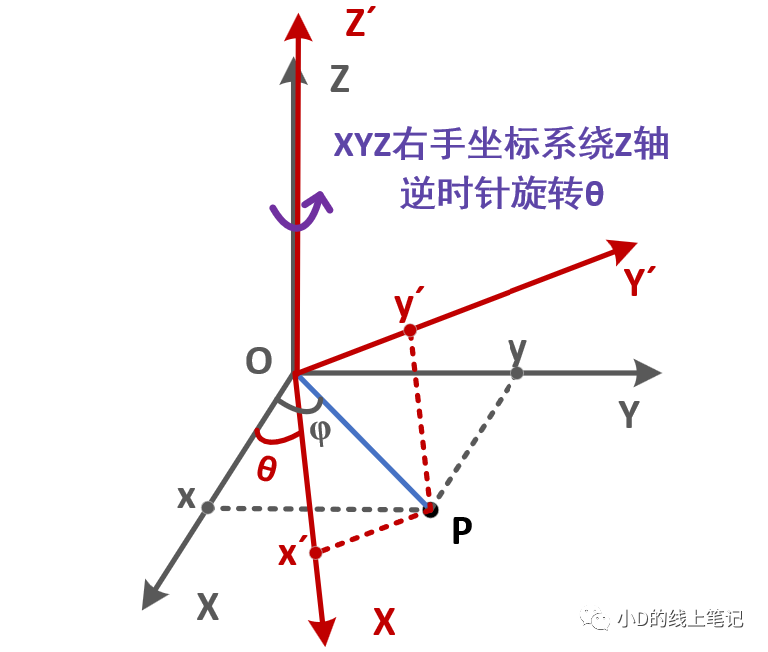
點P在XYZ右手坐標系中的X,Y軸坐標為:
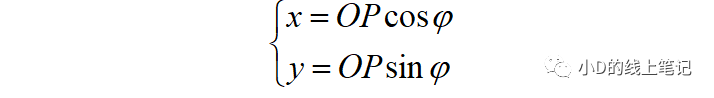
點P在X′Y′Z′坐標系中的x,y坐標為:
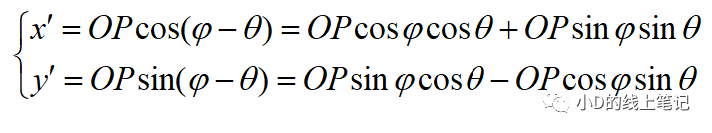
把x,y帶入x′,y′中,同時P點在XYZ中的Z軸坐標與其在X′Y′Z′坐標系中的Z′軸坐標是相等的,所以有:
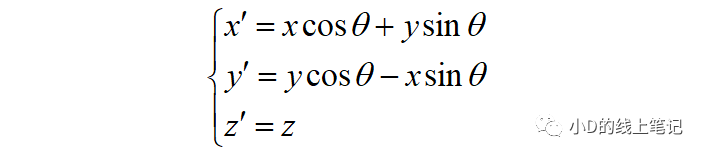
寫成矩陣相乘的形式:
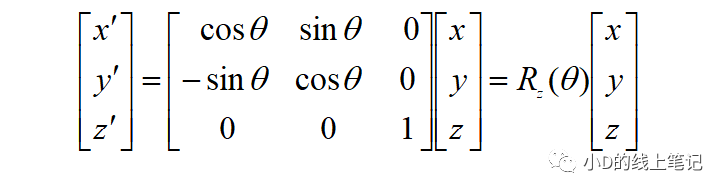
所以,XYZ右手坐標系繞Z軸逆時針旋轉(zhuǎn)θ角的旋轉(zhuǎn)矩陣Rz為:
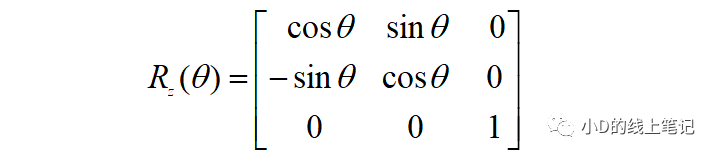
左手坐標系的旋轉(zhuǎn)變換
左手坐標系的旋轉(zhuǎn)過程也是三個,分別是繞X,Y,Z軸旋轉(zhuǎn),左手坐標系在旋轉(zhuǎn)時,通常規(guī)定以順時針旋轉(zhuǎn)方向為正方向。
①XYZ左手坐標系繞X軸順時針旋轉(zhuǎn)θ角
XYZ左手坐標系繞X軸順時針旋轉(zhuǎn)θ角的過程示意圖如下所示:
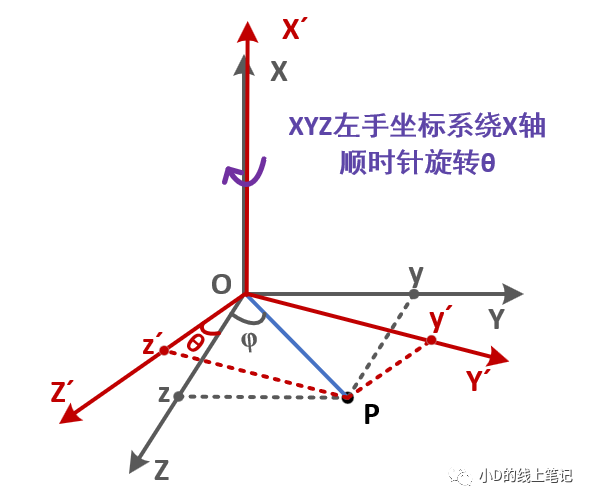
上圖中,點P為空間中任意一點,點P保持不動,XYZ左手坐標系繞X軸順時針旋轉(zhuǎn)θ角形成新的坐標系X′Y′Z′。已知點P在XYZ坐標系中的坐標為(x,y,z),點P在X′Y′Z′中的坐標為(x′,y′,z′),我們要求的是XYZ坐標系變換到X′Y′Z′坐標系這個過程中的旋轉(zhuǎn)矩陣。
從圖中可以看出,點P在XYZ坐標系中的Y,Z軸坐標為:
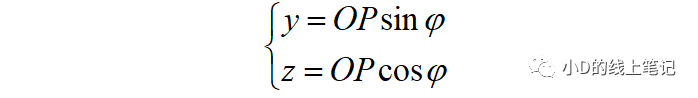
點P在X′Y′Z′坐標系中的Y,Z軸坐標為:
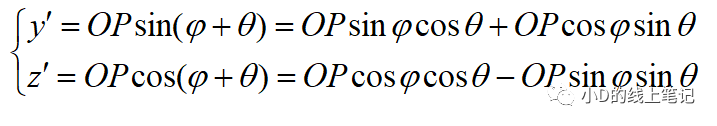
把y,z帶入y′,z′中,同時P點在XYZ中的X軸坐標與其在X′Y′Z′中的X′軸坐標是相等的,所以有:
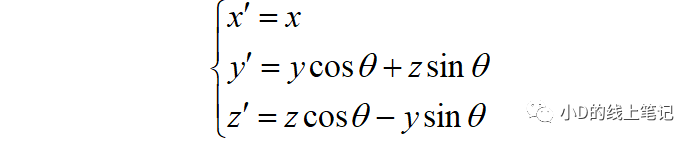
寫成矩陣相乘的形式:
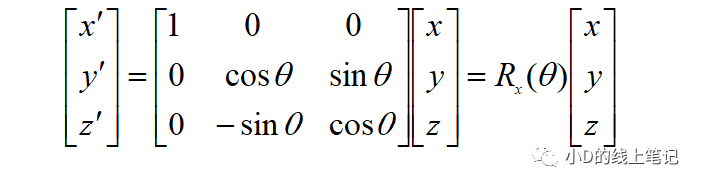
所以,XYZ左手坐標系繞X軸順時針旋轉(zhuǎn)θ角的旋轉(zhuǎn)矩陣為:
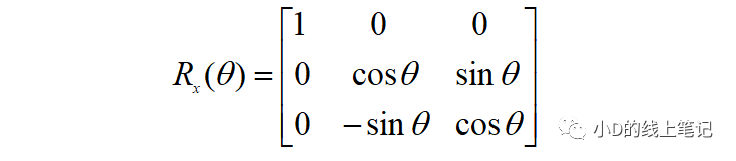
②XYZ左手坐標系繞Y軸順時針旋轉(zhuǎn)θ角
XYZ左手坐標系繞Y軸順時針旋轉(zhuǎn)θ角形成X′Y′Z′坐標系,其過程示意圖如下所示:
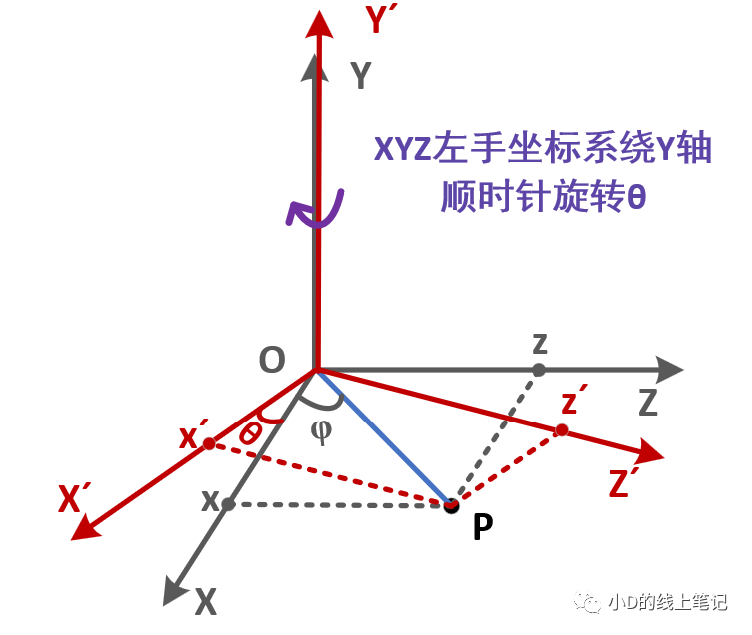
點P在XYZ坐標系中的X,Z軸坐標為:
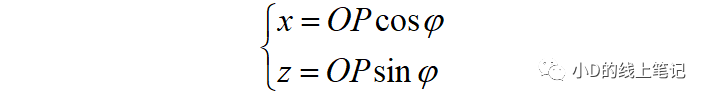
點P在X′Y′Z′坐標系中的X,Z軸坐標為:
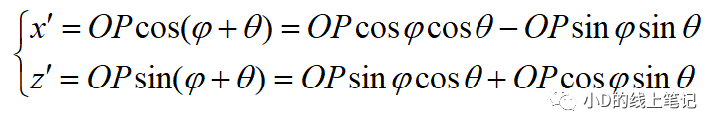
把x,z帶入x′,z′中,同時P點在XYZ中的Y軸坐標與其在X′Y′Z′坐標系中的Y′軸坐標是相等的,所以有:
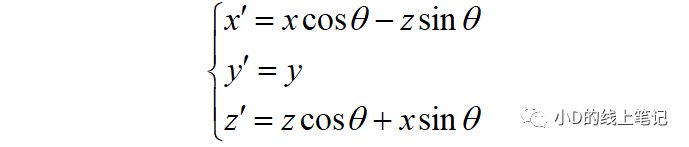
以矩陣形式表示為:
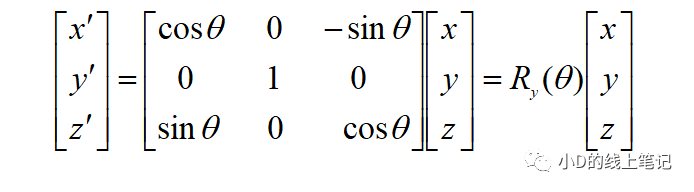
所以,XYZ左手坐標系繞Y軸順時針旋轉(zhuǎn)θ角的旋轉(zhuǎn)矩陣Ry為:
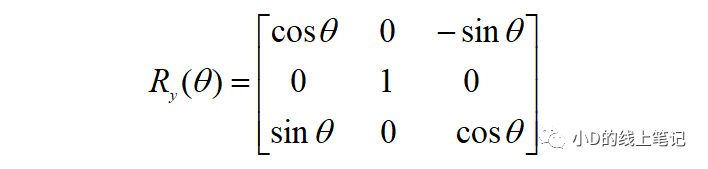
③XYZ左手坐標系繞Z軸順時針旋轉(zhuǎn)θ角
XYZ左手坐標系繞Z軸順時針旋轉(zhuǎn)θ角形成X′Y′Z′坐標系的過程示意圖如下所示:
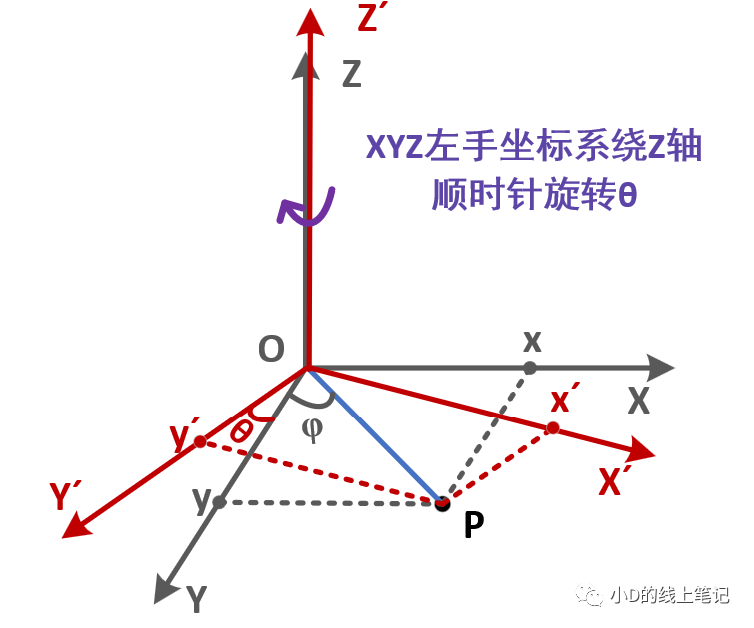
點P在XYZ坐標系中的X,Y軸坐標為:
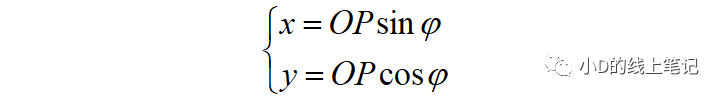
點P在X′Y′Z′坐標系中的X,Y軸坐標為:

把x,y帶入x′,y′中,同時P點在XYZ中的Z軸坐標與其在X′Y′Z′坐標系中的Z′軸坐標是相等的,所以有:
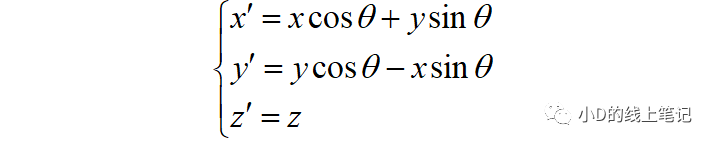
將上式表示成矩陣的形式為:
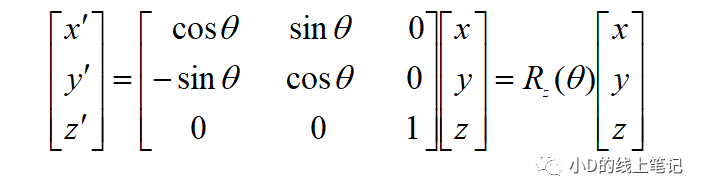
所以,XYZ左手坐標系繞Z軸順時針旋轉(zhuǎn)θ角的旋轉(zhuǎn)矩陣Rz為:
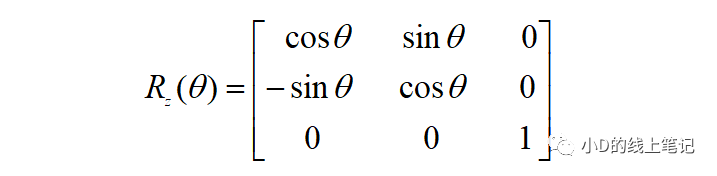
左手坐標系的旋轉(zhuǎn)矩陣到這里就推導完啦。
旋轉(zhuǎn)矩陣的運用
實際中,當我們要推導兩個不同的坐標系,比如地心地固坐標系和北東天、北東天坐標系和機體坐標系等坐標系之間的變換關(guān)系時,就要用到上面的旋轉(zhuǎn)矩陣。一般的方法是,根據(jù)實際的旋轉(zhuǎn)過程,按旋轉(zhuǎn)的先后順序計算旋轉(zhuǎn)矩陣。
比如對于右手坐標系,如果有一個過程是先繞Y軸逆時針旋轉(zhuǎn)α,再繞X軸順時針旋轉(zhuǎn)β,最后繞Z軸逆時針旋轉(zhuǎn)γ,那么最終的旋轉(zhuǎn)矩陣的表達就是:
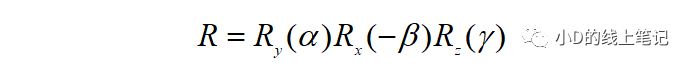
在應用旋轉(zhuǎn)矩陣的過程中,小D還總結(jié)了一個經(jīng)驗:不管是左手坐標系還是右手坐標系,假如繞X軸逆時針旋轉(zhuǎn)θ角,相當于繞X軸順時針旋轉(zhuǎn)2π-θ角,同時也相當于繞X軸順時針旋轉(zhuǎn)-θ角。
旋轉(zhuǎn)矩陣的驗證
推導了這么多公式,那推導結(jié)果是否正確呢?我們可以從《雷達數(shù)據(jù)處理及應用》中找到相關(guān)內(nèi)容:
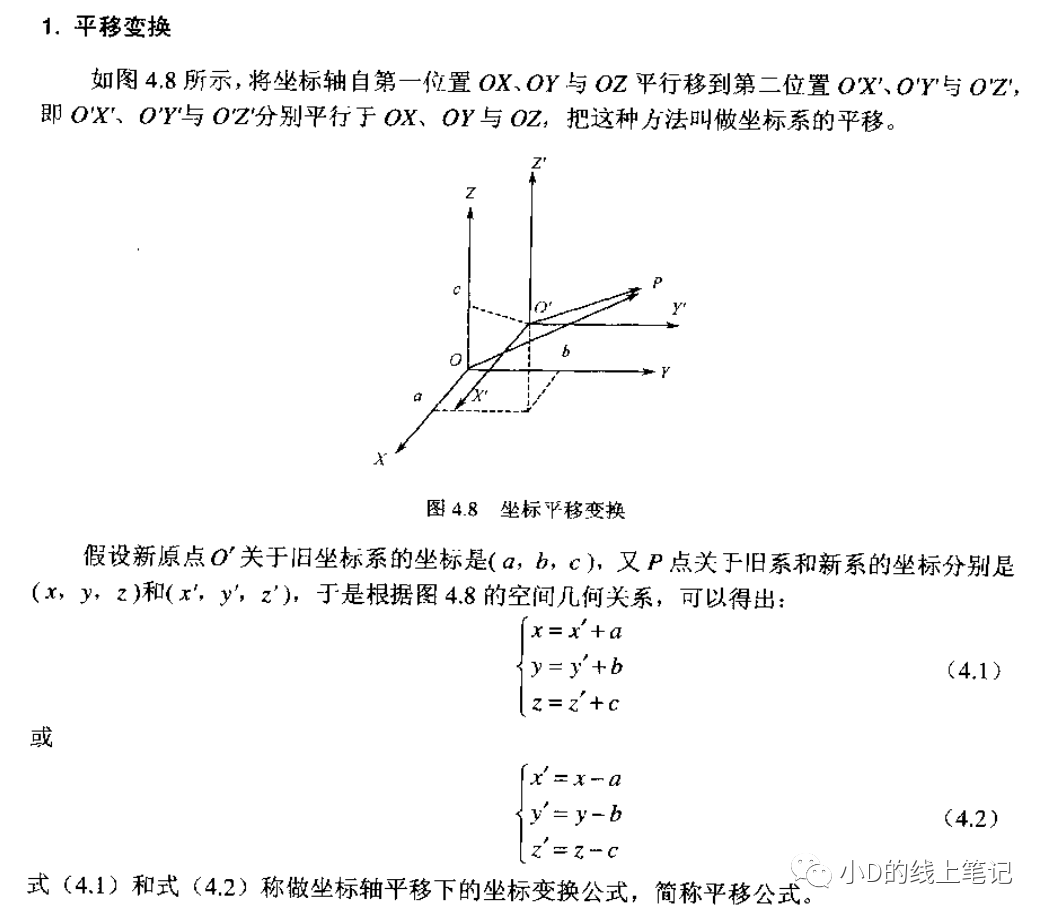


從書中的截圖中可以驗證,自己推導的平移變換以及右手坐標系的旋轉(zhuǎn)矩陣是沒有問題的。但是左手坐標系的推導,小D至今沒有找到相關(guān)文獻,但小D相信肯定是有的。
然后小D向gpt求證,gpt給出的答案是這樣的:
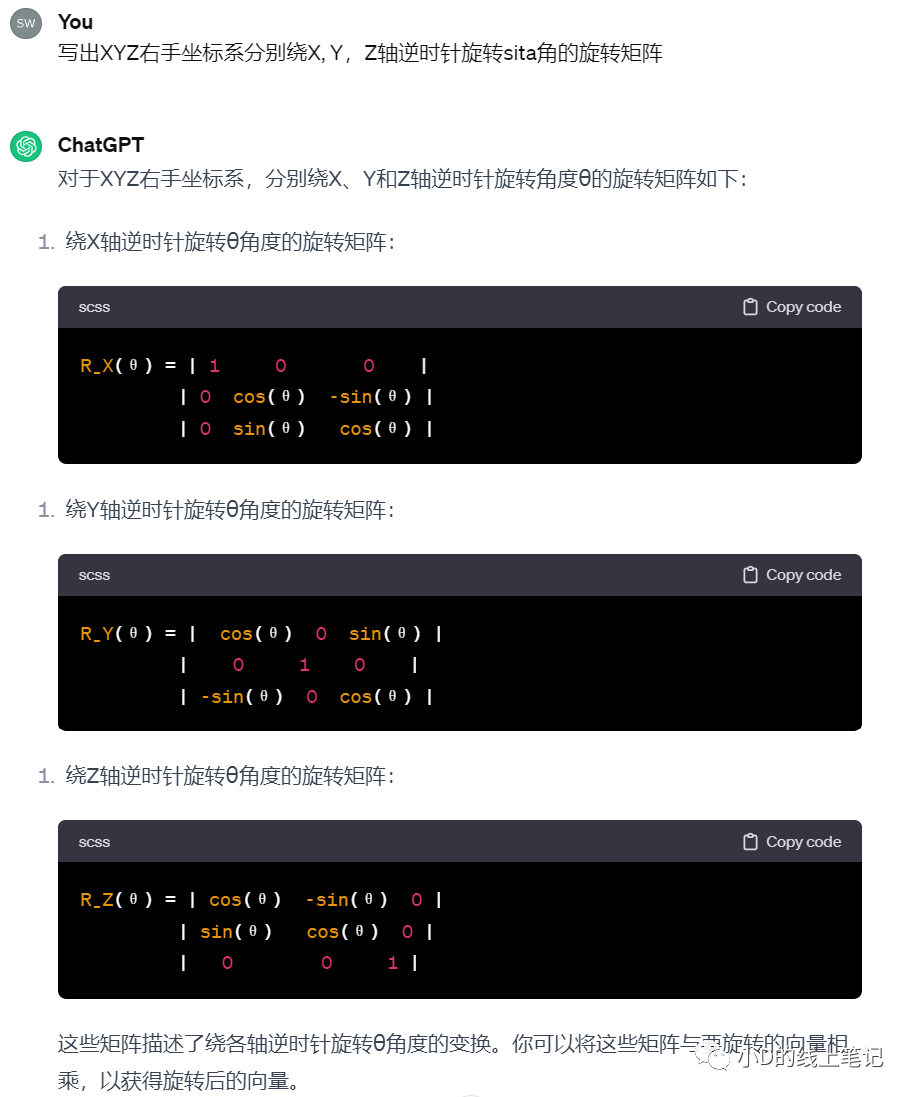
很顯然,gpt給出的右手坐標系的旋轉(zhuǎn)矩陣不是小D上面推導的結(jié)果,也跟書中的結(jié)果不一樣。于是小D又去問了gpt4,gpt4的回答是這樣的:

gpt4的回答和gpt3.5的回答如出一轍,當時小D心想,gpt腦子估計又瓦特了。直到最近,小D看到了一本英文書籍Geometric Transformations for 3D Modeling_Michael Mortenson,小D才明白,原來gpt是沒有正確理解問題,它給出的是坐標系中的點轉(zhuǎn)動,坐標軸不動的情況。這本英文書籍中坐標轉(zhuǎn)換相關(guān)的內(nèi)容是這樣的:





這個時候,小D才明白為什么gpt會給出那樣的答案,因為旋轉(zhuǎn)分為兩種:
①點不動,坐標軸旋轉(zhuǎn),就是小D推導的公式
②坐標軸不動,點旋轉(zhuǎn),就是gpt第一次回答的公式
以另一種方式問它,它就回答對了“點不動,坐標軸旋轉(zhuǎn)”的旋轉(zhuǎn)矩陣正確的公式:


到這里,就驗證了小D推導的坐標轉(zhuǎn)換的所有公式啦。
審核編輯:湯梓紅
-
坐標系
+關(guān)注
關(guān)注
0文章
29瀏覽量
7475 -
三維空間
+關(guān)注
關(guān)注
0文章
19瀏覽量
7696
原文標題:坐標系的平移、旋轉(zhuǎn)變換——超詳細
文章出處:【微信號:FPGA算法工程師,微信公眾號:FPGA算法工程師】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
講座2 信號變換基礎(chǔ) -- 線性空間及正交變換的基本理論
轉(zhuǎn):繞任意空間軸旋轉(zhuǎn)三維圖形
如何使用labview根據(jù)XYZ坐標實時繪制三維曲線
電機控制系統(tǒng)中直角坐標系與極坐標系的優(yōu)勢比較,請問TI是否有現(xiàn)成的demo例程?
CAD制圖軟件新手攻略:坐標系及標注坐標
多電平逆變器三維空間矢量調(diào)制
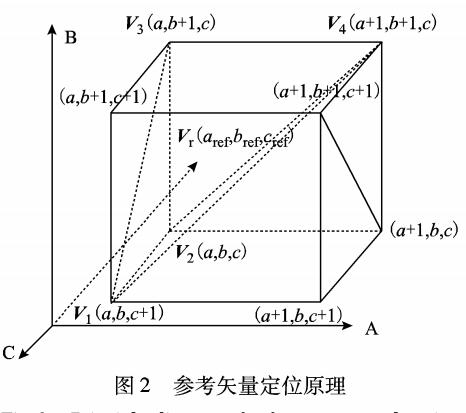
非正交三維坐標系下多電平空間矢量調(diào)制策略
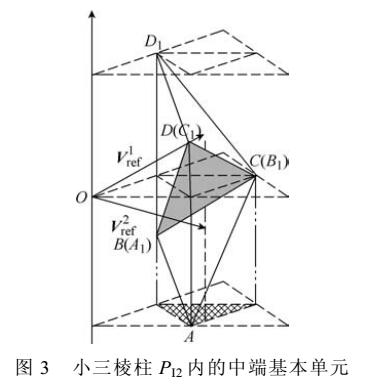
如何使用FPGA實現(xiàn)abc坐標系的三維空間矢量調(diào)制算法
立體倉庫三維空間路徑優(yōu)化方案的介紹
介紹導航坐標系與載體坐標系之間的姿態(tài)旋轉(zhuǎn)矩陣
自動駕駛各個坐標系

焊接機器人坐標系有哪幾種






 三維空間直角坐標系的平移和旋轉(zhuǎn)變換
三維空間直角坐標系的平移和旋轉(zhuǎn)變換











評論