01
什么是傅里葉變換?
一句話概括: “把復雜信號拆成多個簡單正弦波的疊加。” 就像把一道混合光分解成彩虹(七色光),傅里葉變換能把任何波動信號(聲音、圖像、電磁波等)拆解成不同頻率的“正弦波”組合。
02
原理:數學家的“透視眼”
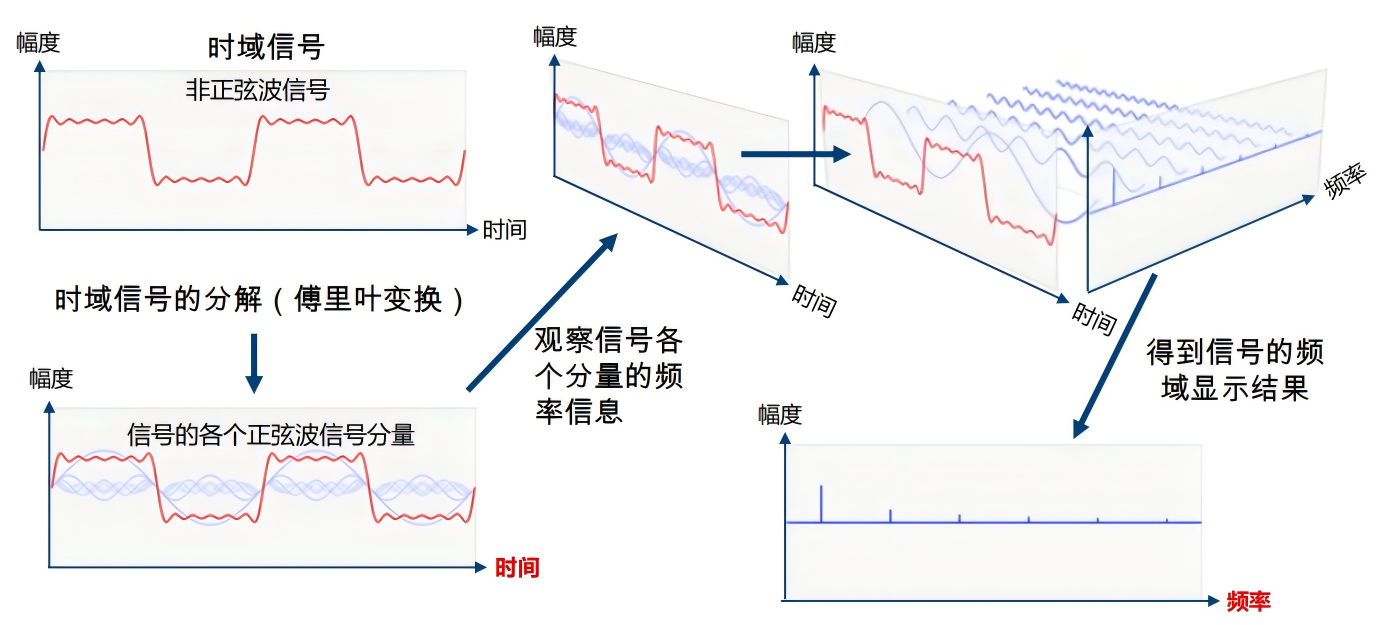
想象你在聽交響樂,同時聽到小提琴、大提琴、長笛… 傅里葉變換就是那個能“分離樂器”的數學工具:
時域信號 → 我們看到的是“振幅隨時間變化”的波形。
頻域信號 → 傅里葉變換后看到的是“每個頻率的強度”。
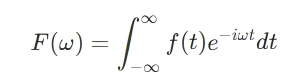 核心公式
核心公式03
為什么偉大?它解決了什么?
信息壓縮:
JPEG圖片、MP3音樂都用它壓縮(保留主要頻率,刪掉人眼/耳不敏感的)。
信號去噪:
心電圖EEG有噪音?濾掉高頻雜波,只留心跳信號。
通信基石:
4G/5G/WiFi 靠它把數據“編碼”到不同頻率傳輸,互不干擾。
圖像增強:
美顏濾鏡的“磨皮”本質是去掉圖像高頻部分(細節皺紋),保留低頻(平滑皮膚)。
04
延伸的應用場景
醫學影像:MRI核磁共振靠它重建人體斷層圖像。
金融分析:股票波動分解成長期趨勢 + 短期震蕩。
天文觀測:從宇宙微波背景輻射中尋找原始頻率信號。
AI語音助手:你的“嗨 Siri”被快速轉成頻域特征識別。
地震波分析:預測石油分布、監測核試驗。
汽車工程領域:傅里葉變換可用于診斷車輛異響問題。其原理在于:所有聲音本質上都是由物體振動產生的。當車輛出現異常噪音時,往往意味著某些零部件在特定工況下發生了非預期的共振。
05
總結
每個系統都有一組確定的共振頻率,這些頻率也被稱為特征頻率,它是系統的固有屬性,如同DNA般刻寫著系統的本質特征。傅里葉變換就像一位翻譯官,它能將時域中紛繁復雜的信號(隨時間舞動的曲線),解碼為頻域中一組組永恒不變的基本元素(特定頻率的正弦波)。
-
正弦波
+關注
關注
11文章
655瀏覽量
56517 -
信號
+關注
關注
11文章
2849瀏覽量
78094 -
傅里葉變換
+關注
關注
6文章
443瀏覽量
43088
發布評論請先 登錄
DSP變換運算-傅里葉變換
小波變換比傅里葉變換好在哪里_小波變換與傅里葉變換詳解

傅里葉變換的介紹傅里葉變換有什么意義和應用






 傅里葉變換的原理及應用
傅里葉變換的原理及應用












評論