【導讀】為了更好地理解神經(jīng)網(wǎng)絡(luò)的運作,今天只為大家解讀神經(jīng)網(wǎng)絡(luò)背后的數(shù)學原理。而作者寫這篇文章的目的一個是為了整理自己學到的知識;第二個目的也是為了分享給大家,如果學習時有困惑難解的知識,希望這篇文章可以有助于大家的學習與理解。對于代數(shù)和微積分相關(guān)內(nèi)容基礎(chǔ)薄弱的小伙伴們,雖然文中涉及不少數(shù)學知識,但我會盡量讓內(nèi)容易于大家理解。
▌解析深度網(wǎng)絡(luò)背后的數(shù)學
如今,已有許多像 Keras, TensorFlow, PyTorch 這樣高水平的專門的庫和框架,我們就不用總擔心矩陣的權(quán)重太多,或是對使用的激活函數(shù)求導時存儲計算的規(guī)模太大這些問題了。基于這些框架,我們在構(gòu)建一個神經(jīng)網(wǎng)絡(luò)時,甚至是一個有著非常復雜的結(jié)構(gòu)的網(wǎng)絡(luò)時,也僅需少量的輸入和代碼就足夠了,極大地提高了效率。無論如何,神經(jīng)網(wǎng)絡(luò)背后的原理方法對于像架構(gòu)選擇、超參數(shù)調(diào)整或者優(yōu)化這樣的任務有著很大的幫助。
圖一 訓練集可視化
舉個例子,我們將利用上圖展示的訓練集數(shù)據(jù)去解決一個二分類問題。從上面的圖可以看出,數(shù)據(jù)點形成了兩個圓,這對于許多傳統(tǒng)的機器學習算法是不容易的,但是現(xiàn)在用一個小的神經(jīng)網(wǎng)絡(luò)就可能很好地解決這個問題了。為了解決這個問題,我們將構(gòu)建一個神經(jīng)網(wǎng)絡(luò):包括五個全連接層,每層都含有不同數(shù)目的單元,結(jié)構(gòu)如下:
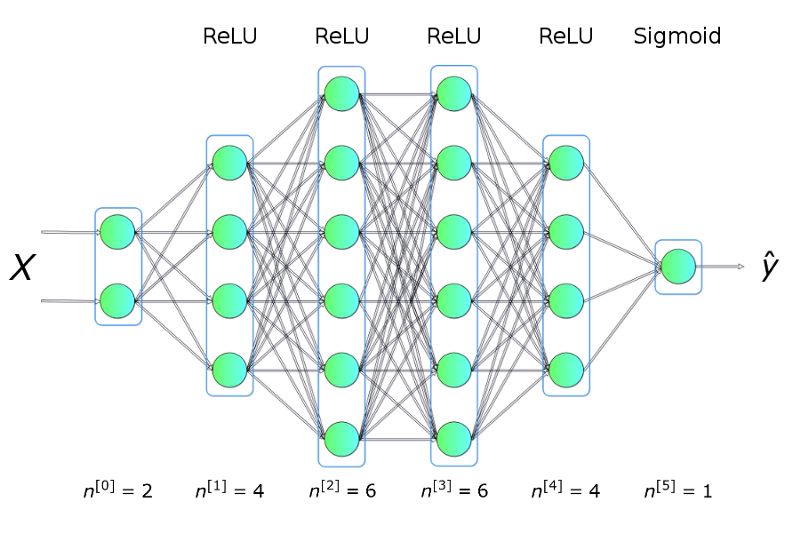
圖二 神經(jīng)網(wǎng)絡(luò)架構(gòu)
其中,隱藏層使用 ReLU 作為激活函數(shù),輸出層使用 Sigmoid。這是一個非常簡單的架構(gòu),但是對于解決并解釋這個問題已經(jīng)足夠了。
用 KERAS 求解
首先,先給大家介紹一個解決方法,使用了一個最受歡迎的機器學習庫—— KERAS 。
fromkeras.modelsimportSequentialfromkeras.layersimportDensemodel=Sequential()model.add(Dense(4,input_dim=2,activation='relu'))model.add(Dense(6,activation='relu'))model.add(Dense(6,activation='relu'))model.add(Dense(4,activation='relu'))model.add(Dense(1,activation='sigmoid'))model.compile(loss='binary_crossentropy',optimizer='adam',metrics=['accuracy'])model.fit(X_train,y_train,epochs=50,verbose=0)
正如我在簡介中提到的,少量的輸入數(shù)據(jù)和代碼就足以構(gòu)建和訓練出一個模型,并且在測試集上的分類精度幾乎達到100%。概括來講,我們的任務其實就是提供與所選架構(gòu)一致的超參數(shù)(層數(shù)、每層的神經(jīng)元數(shù)、激活函數(shù)或者迭代次數(shù))。先給大家展示一個超酷的可視化結(jié)果,是我在訓練過程中得到的:
圖三 訓練中正確分類區(qū)域的可視化
現(xiàn)在我們來解析這背后的原理。
▌什么是神經(jīng)網(wǎng)絡(luò)?
讓我們從關(guān)鍵問題開始:什么是神經(jīng)網(wǎng)絡(luò)?它是一種由生物啟發(fā)的,用來構(gòu)建可以學習并且獨立解釋數(shù)據(jù)中聯(lián)系的計算機程序的方法。如上圖二所示,網(wǎng)絡(luò)就是各層神經(jīng)元的集合,這些神經(jīng)元排列成列,并且相互之間連接,可以進行交流。
▌單個神經(jīng)元
每個神經(jīng)元以一組 x 變量(取值從1到 n )的值作為輸入,計算預測的 y-hat 值。假設(shè)訓練集中含有 m 個樣本,則向量 x 表示其中一個樣本的各個特征的取值。此外,每個單元有自己的參數(shù)集需要學習,包括權(quán)重向量和偏差,分別用 w 和 b 表示。在每次迭代中,神經(jīng)元基于本輪的權(quán)重向量計算向量 x 的加權(quán)平均值,再加上偏差。最后,將計算結(jié)果代入一個非線性激活函數(shù) g。我會在下文中介紹一些最流行的激活函數(shù)。
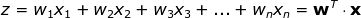

圖四 單個神經(jīng)元
▌單層
現(xiàn)在我們看一下神經(jīng)網(wǎng)絡(luò)中整體的一層是怎么計算的。我們將整合每個單元中的計算,進行向量化,然后寫成矩陣的形式。為了統(tǒng)一符號,我們選取第 l 層寫出矩陣等式,下標 i 表示第 i 個神經(jīng)元。

圖五 單層神經(jīng)網(wǎng)絡(luò)
注意一點:當我們對單個單元寫方程的時候,用到了 x 和 y-hat,它們分別表示特征列向量和預測值。但當我們對整個層寫的時候,要用向量 a 表示相應層的激活值。因此, 向量 x 可以看做第0層輸入層的激活值。每層的各個神經(jīng)元相似地滿足如下等式:

為了清楚起見,以下是第二層的所有表達式:

可見,每層的表達式都是相似的。用 for 循環(huán)來表示很低效,因此為了加速計算速度我們使用了向量化。首先,將權(quán)重向量 w 的轉(zhuǎn)置堆疊成矩陣 W。相似地,將各個神經(jīng)元的偏差也堆在一起組成列向量 b。由此,我們就可以很輕松地寫出一個矩陣等式來表示關(guān)于某一層的所有神經(jīng)元的計算。使用的矩陣和向量維數(shù)表示如下:
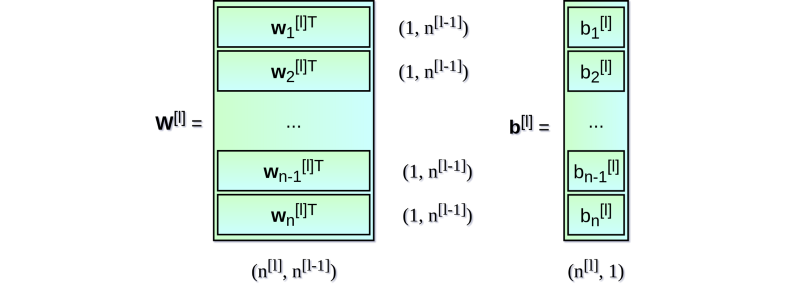
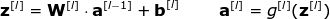
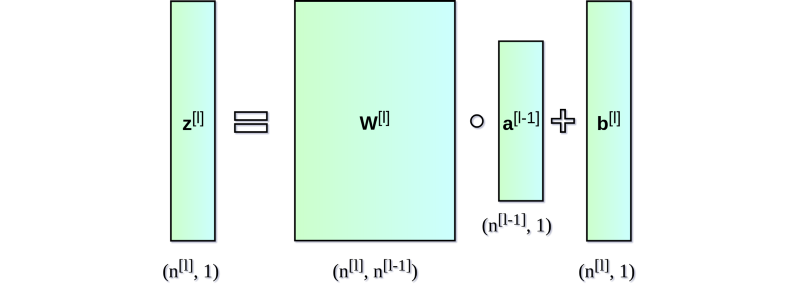
▌多樣本向量化
到目前為止,我們寫出的等式僅包含一個樣本。但在神經(jīng)網(wǎng)絡(luò)的學習過程中,通常會處理一個龐大的數(shù)據(jù)集,可達百萬級的輸入。因此,下一步需要進行多樣本向量化。我們假設(shè)數(shù)據(jù)集中含有 m 個輸入,每個輸入有 nx 個特征。首先,將每層的列向量 x, a, z 分別堆成矩陣 X, A, Z。然后,根據(jù)新的矩陣重寫之前的等式。


▌什么是激活函數(shù)?我們?yōu)槭裁葱枰?/p>
激活函數(shù)是神經(jīng)網(wǎng)絡(luò)的關(guān)鍵元素之一。沒有它們,神經(jīng)網(wǎng)絡(luò)就只是一些線性函數(shù)的組合,其本身也只能是一個線性函數(shù)。我們的模型有復雜度的限制,不能超過邏輯回歸。其中,非線性元保證了更好的適應性,并且能在學習過程中提供一些復雜的函數(shù)。激活函數(shù)對學習的速度也有顯著影響,這也是在選擇時的評判標準之一。圖六展示了一些常用的激活函數(shù)。近年來,隱藏層中使用最廣的激活函數(shù)大概就是 ReLU 了。不過,當我們在做二進制分類問題時,我們有時仍然用 sigmoid,尤其是在輸出層中,我們希望模型返回的值在0到1之間。
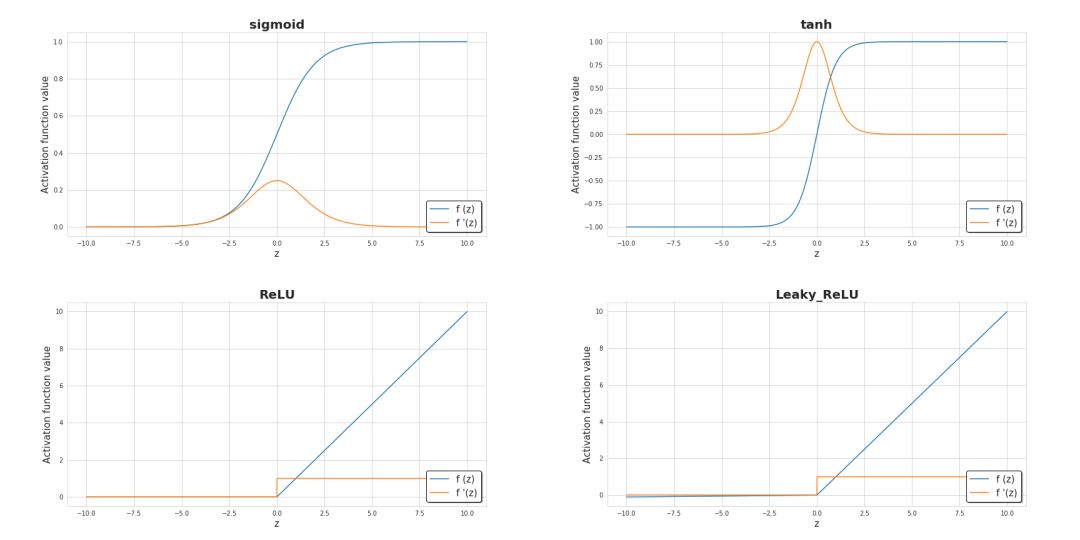
圖六 常用激活函數(shù)及其導數(shù)函數(shù)圖像
▌?chuàng)p失函數(shù)
關(guān)于學習過程進展的基本的信息來源就是損失函數(shù)值了。通常來說,損失函數(shù)可以表示我們離“理想”值還差多遠。在本例中,我們用binary crossentropy(兩元交叉熵)來作為損失函數(shù),不過還有其他的損失函數(shù),需要具體問題具體分析。兩元交叉熵函數(shù)表示如下:
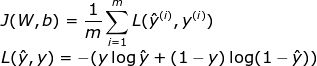
下圖展示了在訓練過程中其值的變化,可見其值隨著迭代次數(shù)如何增加與減少,精度如何提高

圖七 訓練過程中精確度及損失的變化
▌神經(jīng)網(wǎng)絡(luò)如何學習?
學習過程其實就是在不斷地更新參數(shù) W 和 b 的值從而使損失函數(shù)最小化。為此,我們運用微積分以及梯度下降的方法來求函數(shù)的極小。在每次迭代中,我們將分別計算損失函數(shù)對神經(jīng)網(wǎng)絡(luò)中的每個參數(shù)的偏導數(shù)值。對這方面計算不太熟悉的小伙伴,我簡單解釋一下,導數(shù)可以刻畫函數(shù)的(斜率)。我們已經(jīng)知道了怎樣迭代變量會有怎么樣的變化,為了對梯度下降有更直觀的認識,我展示了一個可視化動圖,從中可以看到我們是怎么通過一步步連續(xù)的迭代逼近極小值的。在神經(jīng)網(wǎng)絡(luò)中也是一樣的——每一輪迭代所計算的梯度顯示我們應該移動的方向。而他們間最主要的差別在于,神經(jīng)網(wǎng)絡(luò)需要計算更多的參數(shù)。確切地說,怎么計算如此復雜的導數(shù)呢?
圖八 動態(tài)梯度下降
▌反向傳播算法
反向傳播算法是一種可以計算十分復雜的梯度的算法。在神經(jīng)網(wǎng)絡(luò)中,各參數(shù)的調(diào)整公式如下:
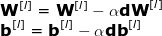
其中,超參數(shù) α 表示學習率,用以控制更新步長。選定學習率是非常重要的——太小,NN 學習得太慢;太大,無法達到極小點。用鏈式法則計算 dW 和 db —— 損失函數(shù)對 W 和 b 的偏導數(shù), dW 和 db 的維數(shù)與 W 和 b 相等。圖九展示了神經(jīng)網(wǎng)絡(luò)中的一系列求導操作,從中可以清楚地看到前向和后向傳播是怎樣共同優(yōu)化損失函數(shù)的。

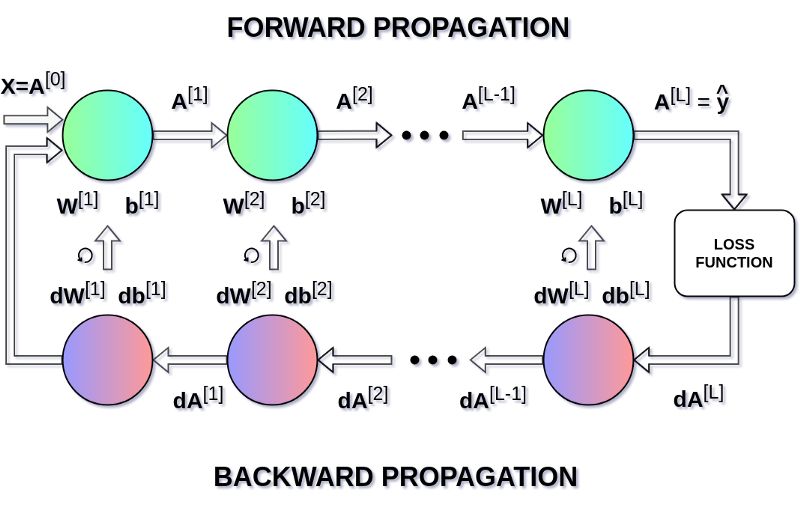
圖九 前向與后向傳播
▌結(jié)論
希望這篇文章對各位小伙伴理解神經(jīng)網(wǎng)絡(luò)內(nèi)部運用的數(shù)學原理有所幫助。當我們使用神經(jīng)網(wǎng)絡(luò)時,理解這個過程的基本原理是很有幫助的。文中講述的內(nèi)容雖然只是冰山一角,但都是我認為最重要的知識點。因此,我強烈建議大家能試著獨立地去編一個小的神經(jīng)網(wǎng)絡(luò),不要依賴框架,僅僅只用 Numpy 嘗試一下。
-
神經(jīng)網(wǎng)絡(luò)
+關(guān)注
關(guān)注
42文章
4812瀏覽量
103215 -
機器學習
+關(guān)注
關(guān)注
66文章
8499瀏覽量
134331
原文標題:解析深度神經(jīng)網(wǎng)絡(luò)背后的數(shù)學原理!
文章出處:【微信號:rgznai100,微信公眾號:rgznai100】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
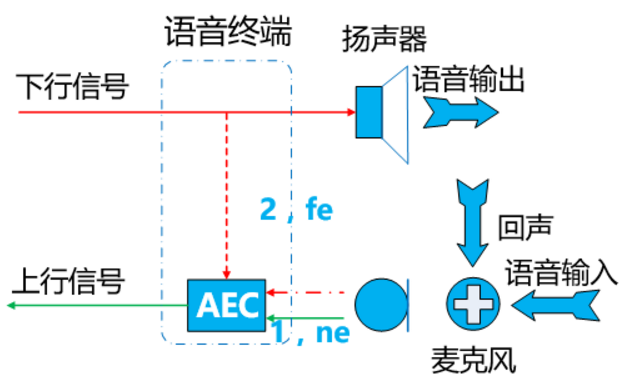
語音視頻社交背后技術(shù)深度解析





 解析深度網(wǎng)絡(luò)背后的數(shù)學以及解析這背后的原理
解析深度網(wǎng)絡(luò)背后的數(shù)學以及解析這背后的原理











評論