CAN調度理論與實踐分析

CAN總線中消息能否按時送達是事關系統安全等問題的重要指標，它要通過調度分析加以驗證。本文介紹CAN調度理論的新研究成果，以及對工程應用的指導意義及其實施難點。具體分為4個部分：Tindell的分析方法和Davis的改進；筆者對Davis算法的簡化；最壞響應時間分析在應用上的一些結果；調度分析在應用上的難處。

關鍵詞? CAN? 調度理論? 響應時間? Davis算法? Tindell算法

　　分布式嵌入式系統是當前嵌入式系統的重要發展方向，因為它能提供更強的性能，節約系統的總體成本。但是由于各單個節點必須有通信網絡相連才能協調地工作，網絡就成了關鍵部分，沒有網絡提供及時正確的數據和命令，就談不上所設計的系統服務了。在汽車的分布式嵌入式系統中，目前主流的通信網絡是CAN總線。CAN是事件觸發的通信協議，它根據消息的優先等級和節點的狀態自動地調度消息的傳送。低優先級的消息會因同時發生的高優先級消息太多而不能及時發送，高優先級消息也有可能由于節點狀態等的影響而丟失。關于CAN的局限問題可見參考文獻[1]。本文主要從調度理論方面討論CAN系統的問題，這些問題與工程應用有非常大的關系，實踐意義很強。

1? Tindell的分析方法和Davis的改進

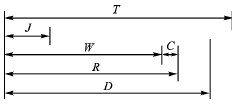
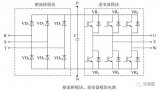
　　1994年，Tindell [23]首先將分析單處理器任務調度方法改造成適用于CAN總線的調度方法，求取消息的最壞響應時間。對于與安全相關的應用，只有對最壞響應時間有確切的掌握，才是合理的。CAN通信在網絡上的實現經過2個階段：通信任務將消息發到發送的通信控制器(CC)，發送的通信控制器將消息發到接收的通信控制器。廣義地講，響應時間是從需產生通信的事件發生到消息到達目標節點的時間，包括發送節點host內的處理時間，host到CC的時間，總線上消息仲裁傳送時間，接收CC到host的處理時間。仲裁獲勝的消息開始傳送后，便不能被中止，所以CAN調度是固定優先級非搶先式任務調度。消息m用到的參數定義如下:

　　Tm ——啟動通信的事件間隔，即周期；
　　Jm——由事件發生到消息開始送CC的時間之最大變化，即抖動；
　　Cm—— 在總線上傳送消息m所需時間（要考慮位填充形成的最大值）；
　　Dm——由應用決定的傳送消息m允許的時限；
　　Rm——實際的最壞傳送時間；
　　Wm——傳送消息m時最壞等待時間。

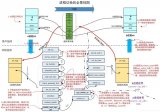
　　它們之間的關系如圖1所示。

圖1? 用于調度分析的時間參數

　　Wm由2部分構成：由低于優先級m的消息（其集合寫為lp(m)）正在總線上傳送而造成的阻塞Bm，和由高于優先級m的消息（其集合寫為hp(m)）在總線上搶先傳送而造成的干擾Im。它們取最大值時就使Wm成為最壞等待時間。

　　為了印刷的方便和易于理解，這里用了不同的寫法，其中頂函數Ceiling返回的是最接近（大于等于）變量的上限整數, τ是1位時間。Ceiling( (Wm+Jk+τ)/Tk)表示在Wm時段內高優先級消息k會出現的最多次數。于是有：

　　Wm取離散值且出現在非線性方程(4)的兩邊，所幸的是其求解并不難。在式(5)中，用W0m=Bm作為初值循環求解即可。

　　式(7)代表最壞等待時間已超時限，消息m不可調度。

　　按優先級降低的次序逐條校驗消息是否可調度，就可驗證整個通信系統是否可調度。

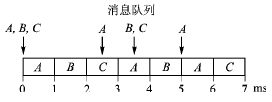
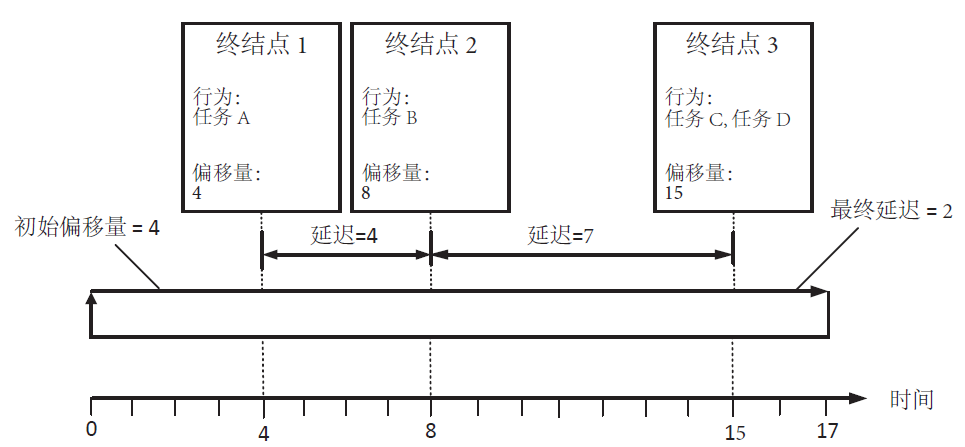
　　在2006年實時網絡會議上，Bril、Davis等人發表了有關Tindell算法有漏洞的文章，后來他們又提出了完整的改進算法[4]。作為反例，表1中消息C用Tindell算法是可調度的，最壞響應時間為3 ms；但第2次消息C的傳送已超時限，如圖2所示。Tindell算法僅考慮了消息C的第1次傳送。

表1? Tindell算法的反例

圖2? 消息C的最壞響應時間為3.5 ms

　　另外，如將消息B和C的周期縮短為3.25 ms，按照Tindell算法，系統由于未求得最大的最壞響應時間，故仍是可調度的，但實際上總線的利用率已超過100%。Davis的方法核心是引入忙周期的概念，再對忙周期內各次傳送的響應時間求最壞值，詳見附錄1。（見本刊網站www.mesnet.com.cn——編者注。）

　　Tindell的開創性工作對后續的研究與應用有巨大的影響，Volcano通信技術公司(現在的Mentor Graphics)以此理論為基礎開發了商用的CAN調度分析軟件。由于漏洞的發現，用戶應檢驗軟件是否有了新的補丁以及用它完成的應用是否受影響。

2? 筆者對Davis算法的簡化

　　Davis算法要先算出忙周期，再在忙周期中消息m多次傳送中尋找最壞等待最大的那次。基于以下考慮，計算可以簡化：

　　在忙周期中，消息m傳送時有高優先級消息進入隊列，使m的后續消息發送前可能插入更多的高優先級消息，代表仍有一個對總線需求的高峰，從而有可能使后面的消息m有更大的最壞響應時間。

　　最壞的情形是消息m剛發送，所有高優先級消息就進入隊列，即領先于發完消息m后的第一個發送空隙的相位達到最大。

　　因此求消息m的最壞響應時間就有兩種可能： 用Bm產生阻塞，像Tindell那樣求消息m的最壞響應時間；由Cm產生阻塞，求下一個消息m的最壞響應時間，下一個消息m的排隊時間為Tm-Jm。

　　簡化方法的優點是減少了計算的次數，從而減少工作量。

　　這種算法與Davis算法中的保守算法有兩點不同：一是用Cm來產生阻塞是真實可能發生的，例如從休眠到上電時消息m比高優先級消息早了一點；二是本算法得到的是確切的而非保守的結果。

　　計算方法：

　　第1次，用公式（5）～（7）計算Wm，得到Wm(0)；

　　第2次，用公式

　　對表1所列的例子，按本節方法有: W0m(1)= Tm-Jm=3.5,W1m(1)=5,W2m(1)=6，W3m(1)=6。所以有Wm(1)=6-3.5=2.5, Wm=2.5,最壞響應時間為3.5 ms，與Davis的結果相同；而按Davis的保守算法，Wm=6。至于系統是否可調度，仍然要求每個消息都可調度。

3? 最壞響應時間分析在應用上的一些結果

3.1? 總線利用率低不能保證可調度性

　　有人憑經驗認為，總線利用率＜30%時，性能便有了保證。其實不然，為了證明這一點，Davis等構造了一個例子，如表2所列。

表2? 總線利用率低與可調度性無直接關系舉例

圖3? n=1時表2消息X的傳送過程

　　當I和L的周期增加到任意大時，其占用的總線時間可以忽略不計。此時總線利用率為：

　　就本例而言，在Ch=Cx=55位（0字節數據）、Ci=135位（8字節數據）、Cl=0時，總線利用率與可調度性的關系如表3所列。

表3? 總線利用率與可調度性的關系

　　例如在總線利用率為9.2%時，對10條消息也不能進行調度。本例中優先級消息的抖動較大，似有點異常。但對偶發的事件消息，其周期可取較長，如考慮限定相鄰消息間的時間時，就相當于本例對T－J的設定，所以也非完全沒有理由。

3.2? 優先級設計策略的討論

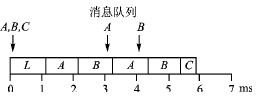
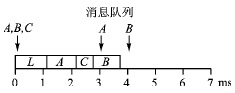
　　一般的說，消息優先級的設置采用時限或（時限－抖動）單調遞變的策略，即時限越短的消息設置的優先級越高，但須用可調度性分析加以驗證，并非這樣做最好[4]。例如，表4優先級的設置為A-B-C，是不能調度的，如圖4所示。此例用11位ID，125 kbps的傳送速率。但將優先級改為A—C—B，按計算結果是可調度的，如圖5所示。

表4? 優先級設置的例子

3.3? 硬件選用對可調度性的影響

　　Tindell [2]比較了兩種通信控制器，認為像82C200一類的通信控制器只有一個發送緩沖器，從而會引起很大的滯后或抖動。例如一個節點有3個消息要傳送，它們的優先級分別為H、 M、 L1，其他節點的消息優先級為L2、 L3、L4。對82C200來說，當要發送H而M已在發送緩沖器里時，就要中止M的發送，而將H寫入，H發完后再將M寫入，由于這些動作都需占用一定時間，而在這些時間里總線可能為其他節點的消息所占用。一次H的搶先，會造成M多次延遲而引起問題（詳見附錄2）。SJA1000與82C200是兼容的通信控制器，國內很多用戶都用它。如果只用于發一種消息，則沒有什么問題；如多個消息共用一個通信控制器，就必須考慮這個問題了。

4? 調度分析在應用上的難處

　　上述分析方法是十分簡化的，對出錯重發情形已有的擴展處理方法，以錯誤的概率模型為基礎，并未考慮節點的狀態。處于bus-off狀態的節點是無法調度的了。因而這種分析總是不完整的，還有待完善。

　　更為困難的是，如果系統不能通過可調度性，那么提供的補救措施極為有限。因為T、C均為實現應用功能所必需的，并可能是產品的現成的特性。此時可能要嘗試修改優先級的分配，包括利用軟件工具自動分配ID，但這與優先級（消息ID）的標準化又背道而馳。同一部件在不同系統應用中要裝入不同的ID，容易混淆，對診斷與維修來說也比較困難。

圖4? 優先級為A—B—C時不可調度

圖5? 優先級為A—C—B時可調度

　　即使進行可調度性分析，必須有所有消息的T、C、J三個參數。其中T、C是供應商會提供的，但J不一定會或不一定能提供。由OEM指定T、C、J，然后由供應商去滿足訂貨要求。雖然有時可行，但隨著專業分工的細化，供應商對控制對象的研究更深刻，所以主動權不全在OEM手里。

　　為了在干擾嚴重的環境下可靠地工作，host一般會起用Watchdog功能來防止程序因走飛而失效。J與Watchdog的正常周期有關，也與Reset后的處理時間有關。如果程序抗干擾設計對數據沒有足夠的保護，則啟動消息發送的本地時鐘和某些與傳送相關的狀態標志會失控，使J也失控。一般的說，設計者現在還無法遍歷所有的走飛狀態從而提供有干擾下的J。如果通過測試確定，與軟件有關的J測試集也是沒保證的。不考慮走飛的J，對CAN調度分析結果可信度有所降低。

　　從上述分析可知，像CAN這種事件觸發的通信協議，為保證消息不錯過時限，必須進行可調度分析；分析后要使不可調度的系統變為可調度，在實踐上比較困難。如果要解決host走飛形成的抖動造成通信失常的后果，只能在控制算法上花力氣了，這在時間觸發協議中也是一樣的。