1 前序遍歷，中序遍歷，后序遍歷；

1.1 前序遍歷

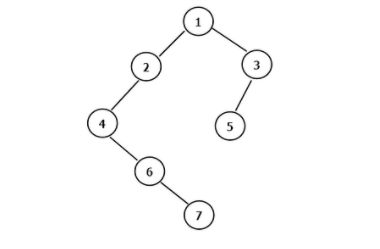
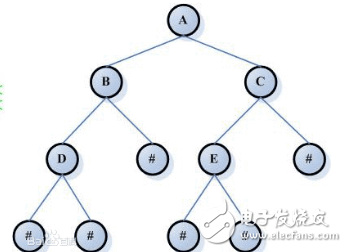
對于當前結(jié)點，先輸出該結(jié)點，然后輸出它的左孩子，最后輸出它的右孩子。以上圖為例，遞歸的過程如下：

輸出 1，接著左孩子；

輸出 2，接著左孩子；

輸出 4，左孩子為空，再接著右孩子；

輸出 6，左孩子為空，再接著右孩子；

輸出 7，左右孩子都為空，此時 2 的左子樹全部輸出，2 的右子樹為空，此時 1 的左子樹全部輸出，接著 1 的右子樹；

輸出 3，接著左孩子；

輸出 5，左右孩子為空，此時 3 的左子樹全部輸出，3 的右子樹為空，至此 1 的右子樹全部輸出，結(jié)束。

而非遞歸版本只是利用 stack 模擬上述過程而已，遞歸的過程也就是出入棧的過程。

/*前序遍歷遞歸版*/
voidPreOrderRec(Node*node)
{
if(node==nullptr)
return;
cout<data<left);//然后輸出左孩子
PreOrderRec(node->right);//最后輸出右孩子
}

/*前序遍歷非遞歸版*/
voidPreOrderNonRec(Node*node)
{
if(node==nullptr)
return;

stackS;
cout<data<left;

while(!S.empty()||node)
{
while(node)
{
cout<data<left;//然后輸出左孩子
}//while結(jié)束意味著左孩子已經(jīng)全部輸出

node=S.top()->right;//最后輸出右孩子
S.pop();
}
}

1.2 中序遍歷

對于當前結(jié)點，先輸出它的左孩子，然后輸出該結(jié)點，最后輸出它的右孩子。以（1.1）圖為例：

1-->2-->4，4 的左孩子為空，輸出 4，接著右孩子；

6 的左孩子為空，輸出 6，接著右孩子；

7 的左孩子為空，輸出 7，右孩子也為空，此時 2 的左子樹全部輸出，輸出 2，2 的右孩子為空，此時 1 的左子樹全部輸出，輸出 1，接著 1 的右孩子；

3-->5，5 左孩子為空，輸出 5，右孩子也為空，此時 3 的左子樹全部輸出，而 3 的右孩子為空，至此 1 的右子樹全部輸出，結(jié)束。

/*中序遍歷遞歸版*/
voidInOrderRec(Node*node)
{
if(node==nullptr)
return;

InOrderRec(node->left);//先輸出左孩子
cout<data<right);//最后輸出右孩子
}

/*前序遍歷非遞歸版*/
voidInOrderNonRec(Node*node)
{
if(node==nullptr)
return;

stackS;
S.push(node);
node=node->left;

while(!S.empty()||node)
{
while(node)
{
S.push(node);
node=node->left;
}//while結(jié)束意味著左孩子為空

cout<data<right;//左孩子全部輸出，當前結(jié)點也輸出后，最后輸出右孩子
S.pop();
}
}

1.3 后序遍歷

對于當前結(jié)點，先輸出它的左孩子，然后輸出它的右孩子，最后輸出該結(jié)點。依舊以（1.1）圖為例：

1->2->4->6->7，7 無左孩子，也無右孩子，輸出 7，此時 6 無左孩子，而 6 的右子樹也全部輸出，輸出 6，此時 4 無左子樹，而 4 的右子樹已全部輸出，接著輸出 4，此時 2 的左子樹全部輸出，且 2 無右子樹，輸出 2，此時 1 的左子樹全部輸出，接著轉(zhuǎn)向右子樹；

3->5，5 無左孩子，也無右孩子，輸出 5，此時 3 的左子樹全部輸出，且 3 無右孩子，輸出 3，此時 1 的右子樹全部輸出，輸出 1，結(jié)束。

非遞歸版本中，對于一個結(jié)點，如果我們要輸出它，只有它既沒有左孩子也沒有右孩子或者它有孩子但是它的孩子已經(jīng)被輸出（由此設(shè)置 pre 變量）。若非上述兩種情況，則將該結(jié)點的右孩子和左孩子依次入棧，這樣就保證了每次取棧頂元素的時候,先依次遍歷左子樹和右子樹。

/*后序遍歷遞歸版*/
voidPostOrderRec(Node*node)
{
if(node==nullptr)
return;

PostOrderRec(node->left);//先輸出左孩子
PostOrderRec(node->right);//然后輸出右孩子
cout<data<S;
S.push(node);

while(!S.empty())
{
node=S.top();

if((!node->left&&!node->right)||//第一個輸出的必是無左右孩子的葉子結(jié)點，只要第一個結(jié)點輸出，
(pre &&(pre == node->left || pre == node->right)))//以后的 pre 就不會是空。此處的判斷語句加入一個 pre，只是用來
{//確保可以正確輸出第一個結(jié)點。
cout<data<right)
S.push(node->right);//先進右孩子，再進左孩子，取出來的才是左孩子
if(node->left)
S.push(node->left);
}
}
}

2 層次遍歷

voidLevelOrder(Node*node)
{
Node*p=node;
queueQ;//隊列
Q.push(p);

while(!Q.empty())
{
p=Q.front();
cout<data<left)
Q.push(p->left);//注意順序，先進左孩子
if(p->right)
Q.push(p->right);
}
}

3 求樹的結(jié)點數(shù)

intCountNodes(Node*node)
{
if(node==nullptr)
return0;

returnCountNodes(node->left)+CountNodes(node->right)+1;
}

4 求樹的葉子數(shù)

intCountLeaves(Node*node)
{
if(node==nullptr)
return0;

if(!node->left&&!node->right)
return1;

returnCountLeaves(node->left)+CountLeaves(node->right);
}

5 求樹的深度

intGetDepth(Node*node)
{
if(node==nullptr)
return0;

intleft_depth=GetDepth(node->left)+1;
intright_depth=GetDepth(node->right)+1;

returnleft_depth>right_depth?left_depth:right_depth;
}

6 求二叉樹第k層的結(jié)點個數(shù)

intGetKLevel(Node*node,intk)
{
if(node==nullptr)
return0;

if(k==1)
return1;

returnGetKLevel(node->left,k-1)+GetKLevel(node->right,k-1);
}

7 判斷兩棵二叉樹是否結(jié)構(gòu)相同

不考慮數(shù)據(jù)內(nèi)容。結(jié)構(gòu)相同意味著對應的左子樹和對應的右子樹都結(jié)構(gòu)相同。

boolStructureCmp(Node*node1,Node*node2)
{
if(node1==nullptr&&node2==nullptr)
returntrue;
elseif(node1==nullptr||node2==nullptr)
returnfalse;

returnStructureCmp(node1->left,node2->left)&&Str1uctureCmp(node1->right,node2->right);
}

8 求二叉樹的鏡像

對于每個結(jié)點，我們交換它的左右孩子即可。

voidMirror(Node*node)
{
if(node==nullptr)
return;

Node*temp=node->left;
node->left=node->right;
node->right=temp;

Mirror(node->left);
Mirror(node->right);
}

9 求兩個結(jié)點的最低公共祖先結(jié)點

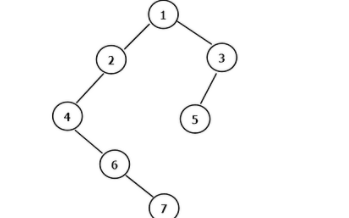
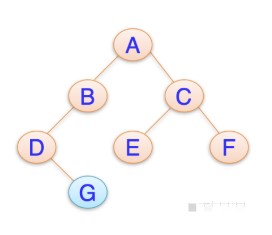
最低公共祖先，即 LCA（Lowest Common Ancestor），見下圖：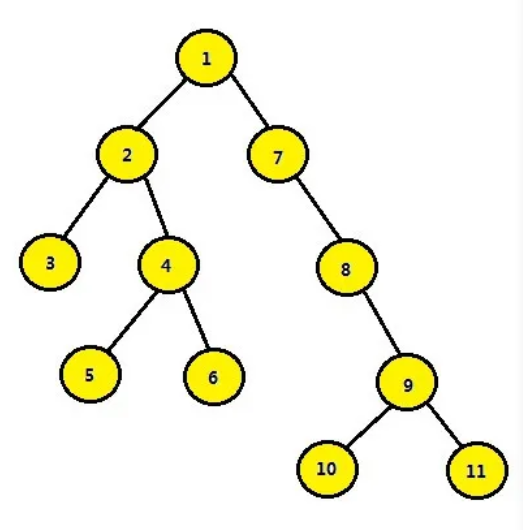



結(jié)點 3 和結(jié)點 4 的最近公共祖先是結(jié)點 2，即 LCA(3,4)=2。在此，需要注意到當兩個結(jié)點在同一棵子樹上的情況，如結(jié)點 3 和結(jié)點 2 的最近公共祖先為 2，即 LCA(3,2)=2。同理 LCA(5,6)=4，LCA(6,10)=1。

Node*FindLCA(Node*node,Node*target1,Node*target2)
{
if(node==nullptr)
returnnullptr;
if(node==target1||node==target2)
returnnode;

Node*left=FindLCA(node->left,target1,target2);
Node*right=FindLCA(node->right,target1,target2);
if(left&&right)//分別在左右子樹
returnnode;

returnleft?left:right;//都在左子樹或右子樹
}

10 求任意兩結(jié)點距離

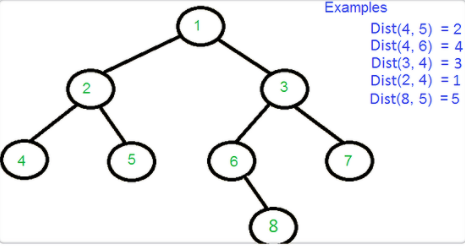
首先找到兩個結(jié)點的 LCA，然后分別計算 LCA 與它們的距離，最后相加即可。

intFindLevel(Node*node,Node*target)
{
if(node==nullptr)
return-1;
if(node==target)
return0;

intlevel=FindLevel(node->left,target);//先在左子樹找
if(level==-1)
level=FindLevel(node->right,target);//如果左子樹沒找到，在右子樹找

if(level!=-1)//找到了，回溯
returnlevel+1;

return-1;//如果左右子樹都沒找到
}

intDistanceNodes(Node*node,Node*target1,Node*target2)
{
Node*lca=FindLCA(node,target1,target2);//找到最低公共祖先結(jié)點
intlevel1=FindLevel(lca,target1);
intlevel2=FindLevel(lca,target2);

returnlevel1+level2;
}

11 找出二叉樹中某個結(jié)點的所有祖先結(jié)點

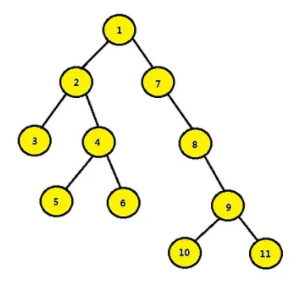
如果給定結(jié)點 5，則其所有祖先結(jié)點為 4,2,1。

boolFindAllAncestors(Node*node,Node*target)
{
if(node==nullptr)
returnfalse;
if(node==target)
returntrue;

if(FindAllAncestors(node->left,target)||FindAllAncestors(node->right,target))//找到了
{
cout<data<

	

	12 不使用遞歸和棧遍歷二叉樹

	1968 年，高德納（Donald Knuth）提出一個問題：是否存在一個算法，它不使用棧也不破壞二叉樹結(jié)構(gòu)，但是可以完成對二叉樹的遍歷？隨后 1979 年，James H. Morris 提出了二叉樹線索化，解決了這個問題。（根據(jù)這個概念我們又提出了一個新的數(shù)據(jù)結(jié)構(gòu)，即線索二叉樹，因線索二叉樹不是本文要介紹的內(nèi)容，所以有興趣的朋友請移步線索二叉樹）

	前序，中序，后序遍歷，不管是遞歸版本還是非遞歸版本，都用到了一個數(shù)據(jù)結(jié)構(gòu)--棧，為何要用棧？那是因為其它的方式?jīng)]法記錄當前結(jié)點的 parent,而如果在每個結(jié)點的結(jié)構(gòu)里面加個 parent 分量顯然是不現(xiàn)實的，而線索化正好解決了這個問題，其含義就是利用結(jié)點的右孩子空指針，指向該結(jié)點在中序序列中的后繼。下面具體來看看如何使用線索化來完成對二叉樹的遍歷。




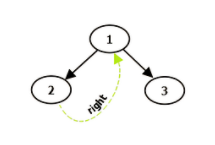
	先看前序遍歷，步驟如下：

	如果當前結(jié)點的左孩子為空，則輸出當前結(jié)點并將其右孩子作為當前結(jié)點；

	如果當前結(jié)點的左孩子不為空，在當前結(jié)點的左子樹中找到當前結(jié)點在中序遍歷下的前驅(qū)結(jié)點；

	2.1如果前驅(qū)結(jié)點的右孩子為空，將它的右孩子設(shè)置為當前結(jié)點，輸出當前結(jié)點并把當前結(jié)點更新為當前結(jié)點的左孩子；

	2.2如果前驅(qū)結(jié)點的右孩子為當前結(jié)點，將它的右孩子重新設(shè)為空，當前結(jié)點更新為當前結(jié)點的右孩子；

	重復以上步驟 1 和 2，直到當前結(jié)點為空。

	
/*前序遍歷*/
voidPreOrderMorris(Node*root)
{
Node*cur=root;
Node*pre=nullptr;

while(cur)
{
if(cur->left==nullptr)//步驟1
{
cout<data<right;
}
else
{
pre=cur->left;
while(pre->right&&pre->right!=cur)//步驟2，找到cur的前驅(qū)結(jié)點
pre=pre->right;

if(pre->right==nullptr)//步驟2.1，cur未被訪問，將cur結(jié)點作為其前驅(qū)結(jié)點的右孩子
{
cout<data<right=cur;
cur=cur->left;
}
else//步驟2.2，cur已被訪問，恢復樹的原有結(jié)構(gòu)，更改right指針
{
pre->right=nullptr;
cur=cur->right;
}
}
}
}

再來看中序遍歷，和前序遍歷相比只改動一句代碼，步驟如下：

	

	如果當前結(jié)點的左孩子為空，則輸出當前結(jié)點并將其右孩子作為當前結(jié)點；

	如果當前結(jié)點的左孩子不為空，在當前結(jié)點的左子樹中找到當前結(jié)點在中序遍歷下的前驅(qū)結(jié)點；

	2.1. 如果前驅(qū)結(jié)點的右孩子為空，將它的右孩子設(shè)置為當前結(jié)點，當前結(jié)點更新為當前結(jié)點的左孩子；

	2.2. 如果前驅(qū)結(jié)點的右孩子為當前結(jié)點，將它的右孩子重新設(shè)為空，輸出當前結(jié)點，當前結(jié)點更新為當前結(jié)點的右孩子；

	重復以上步驟 1 和 2，直到當前結(jié)點為空。

	
/*中序遍歷*/
voidInOrderMorris(Node*root)
{
Node*cur=root;
Node*pre=nullptr;

while(cur)
{
if(cur->left==nullptr)//（1）
{
cout<data<right;
}
else
{
pre=cur->left;
while(pre->right&&pre->right!=cur)//（2），找到cur的前驅(qū)結(jié)點
pre=pre->right;

if(pre->right==nullptr)//（2.1），cur未被訪問，將cur結(jié)點作為其前驅(qū)結(jié)點的右孩子
{
pre->right=cur;
cur=cur->left;
}
else//（2.2），cur已被訪問，恢復樹的原有結(jié)構(gòu)，更改right指針
{
cout<data<right=nullptr;
cur=cur->right;
}
}
}
}


	

	最后看下后序遍歷，后序遍歷有點復雜，需要建立一個虛假根結(jié)點 dummy，令其左孩子是 root。并且還需要一個子過程，就是倒序輸出某兩個結(jié)點之間路徑上的各個結(jié)點。

	


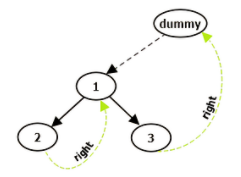
	步驟如下：

	如果當前結(jié)點的左孩子為空，則將其右孩子作為當前結(jié)點；

	如果當前結(jié)點的左孩子不為空，在當前結(jié)點的左子樹中找到當前結(jié)點在中序遍歷下的前驅(qū)結(jié)點；

	2.1. 如果前驅(qū)結(jié)點的右孩子為空，將它的右孩子設(shè)置為當前結(jié)點，當前結(jié)點更新為當前結(jié)點的左孩子；

	2.2. 如果前驅(qū)結(jié)點的右孩子為當前結(jié)點，將它的右孩子重新設(shè)為空，倒序輸出從當前結(jié)點的左孩子到該前驅(qū)結(jié)點這條路徑上的所有結(jié)點，當前結(jié)點更新為當前結(jié)點的右孩子；

	重復以上步驟 1 和 2，直到當前結(jié)點為空。

	
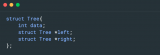
structNode
{
intdata;
Node*left;
Node*right;
Node(intdata_,Node*left_,Node*right_)
{
data=data_;
left=left_;
right=right_;
}
};

voidReversePrint(Node*from,Node*to)
{
if(from==to)
{
cout<data<right,to);
cout<data<left==nullptr)//步驟1
cur=cur->right;
else
{
pre=cur->left;
while(pre->right&&pre->right!=cur)//步驟2，找到cur的前驅(qū)結(jié)點
pre=pre->right;

if(pre->right==nullptr)//步驟2.1，cur未被訪問，將cur結(jié)點作為其前驅(qū)結(jié)點的右孩子
{
pre->right=cur;
cur=cur->left;
}
else//步驟2.2，cur已被訪問，恢復樹的原有結(jié)構(gòu)，更改right指針
{
pre->right=nullptr;
ReversePrint(cur->left,pre);
cur=cur->right;
}
}
}
}


	

	dummy 用的非常巧妙，建議讀者配合上面的圖模擬下算法流程。

	13 二叉樹前序中序推后序

				方式
			

				序列
		

				前序
			

				[1 2 4 7 3 5 8 9 6]
		

				中序
			

				[4 7 2 1 8 5 9 3 6]
		

				后序
			

				[7 4 2 8 9 5 6 3 1]
		

	以上面圖表為例，步驟如下：

	根據(jù)前序可知根結(jié)點為1；

	根據(jù)中序可知 4 7 2 為根結(jié)點 1 的左子樹和 8 5 9 3 6 為根結(jié)點 1 的右子樹；

	遞歸實現(xiàn)，把 4 7 2 當做新的一棵樹和 8 5 9 3 6 也當做新的一棵樹；

	在遞歸的過程中輸出后序。

	
/*前序遍歷和中序遍歷結(jié)果以長度為n的數(shù)組存儲，pos1為前序數(shù)組下標，pos2為后序下標*/

intpre_order_arry[n];
intin_order_arry[n];

voidPrintPostOrder(intpos1,intpos2,intn)
{
if(n==1)
{
cout<

	

	當然我們也可以根據(jù)前序和中序構(gòu)造出二叉樹，進而求出后序。

	
/*該函數(shù)返回二叉樹的根結(jié)點*/
Node*Create(intpos1,intpos2,intn)
{
Node*p=nullptr;

for(inti=0;ileft=Create(pos1+1,pos2,i);
p->right=Create(pos1+i+1,pos2+i+1,n-i-1);
returnp;
}
}

returnp;
}


	

	14 判斷二叉樹是不是完全二叉樹

	若設(shè)二叉樹的深度為 h，除第 h 層外，其它各層 (1～h-1) 的結(jié)點數(shù)都達到最大個數(shù)，第 h 層所有的結(jié)點都連續(xù)集中在最左邊，這就是完全二叉樹（Complete Binary Tree）。如下圖：



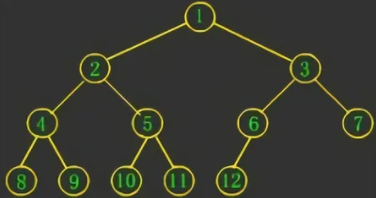
	首先若一個結(jié)點只有右孩子，肯定不是完全二叉樹；其次若只有左孩子或沒有孩子，那么接下來的所有結(jié)點肯定都沒有孩子，否則就不是完全二叉樹，因此設(shè)置 flag 標記變量。

	
boolIsCBT(Node*node)
{
boolflag=false;
queueQ;
Q.push(node);

while(!Q.empty())
{
Node*p=Q.front();
Q.pop();

if(flag)
{
if(p->left||p->right)
returnfalse;
}
else
{
if(p->left&&p->right)
{
Q.push(p->left);
Q.push(p->right);
}
elseif(p->right)//只有右結(jié)點
returnfalse;
elseif(p->left)//只有左結(jié)點
{
Q.push(p->left);
flag=true;
}
else//沒有結(jié)點
flag=true;
}
}

returntrue;
}


	

	15 判斷是否是二叉查找樹的后序遍歷結(jié)果

	在后續(xù)遍歷得到的序列中，最后一個元素為樹的根結(jié)點。從頭開始掃描這個序列，比根結(jié)點小的元素都應該位于序列的左半部分；從第一個大于跟結(jié)點開始到跟結(jié)點前面的一個元素為止，所有元素都應該大于跟結(jié)點，因為這部分元素對應的是樹的右子樹。

	根據(jù)這樣的劃分，把序列劃分為左右兩部分，我們遞歸地確認序列的左、右兩部分是不是都是二元查找樹。

	
intarray[n];//長度為n的序列，注意begin和end遵循的是左閉右閉原則

boolIsSequenceOfBST(intbegin,intend)
{
if(end-begin<=?0)
????????return?true;

????int?root_data?=?array[end];??//?數(shù)組尾元素為根結(jié)點

????int?i?=?begin;
????for?(;?array[i]?

	

	16 給定一個二叉查找樹中的結(jié)點（存在一個指向父親結(jié)點的指針），找出在中序遍歷下它的后繼和前驅(qū)

	一棵二叉查找樹的中序遍歷序列，正好是升序序列。假如根結(jié)點的父結(jié)點為 nullptr，則：

	如果當前結(jié)點有右孩子，則后繼結(jié)點為這個右孩子的最左孩子；

	如果當前結(jié)點沒有右孩子；

	2.1. 當前結(jié)點為根結(jié)點，返回 nullptr；

	2.2. 當前結(jié)點只是個普通結(jié)點，也就是存在父結(jié)點；

	2.2.1. 當前結(jié)點是父親結(jié)點的左孩子，則父親結(jié)點就是后繼結(jié)點；

	2.2.2. 當前結(jié)點是父親結(jié)點的右孩子，沿著父親結(jié)點往上走，直到 n-1 代祖先是 n 代祖先的左孩子，則后繼為 n 代祖先或遍歷到根結(jié)點也沒找到符合的，則當前結(jié)點就是中序遍歷的最后一個結(jié)點，返回 nullptr。

	
/*求后繼結(jié)點*/
Node*Increment(Node*node)
{
if(node->right)//步驟1
{
node=node->right;
while(node->left)
node=node->left;
returnnode;
}
else//步驟2
{
if(node->parent==nullptr)//步驟2.1
returnnullptr;
Node*p=node->parent;//步驟2.2
if(p->left==node)//步驟2.2.1
returnp;
else//步驟2.2.2
{
while(p->right==node)
{
node=p;
p=p->parent;
if(p==nullptr)
returnnullptr;
}
returnp;
}
}
}


	

	仔細觀察上述代碼，總覺得有點啰嗦。比如，過多的 return，步驟 2 的層次太多。綜合考慮所有情況，改進代碼如下：

	
Node*Increment(Node*node)
{
if(node->right)
{
node=node->right;
while(node->left)
node=node->left;
}
else
{
Node*p=node->parent;
while(p&&p->right==node)
{
node=p;
p=p->parent;
}
node=p;
}

returnnode;
}


	

	上述的代碼是基于結(jié)點有 parent 指針的，若題意要求沒有 parent 呢？網(wǎng)上也有人給出了答案，個人覺得沒有什么價值，有興趣的朋友可以到這里查看。

	而求前驅(qū)結(jié)點的話，只需把上述代碼的 left 與 right 互調(diào)即可，很簡單。

	17 二分查找樹轉(zhuǎn)化為排序的循環(huán)雙鏈表

	二分查找樹的中序遍歷即為升序排列，問題就在于如何在遍歷的時候更改指針的指向。一種簡單的方法時，遍歷二分查找樹，將遍歷的結(jié)果放在一個數(shù)組中，之后再把該數(shù)組轉(zhuǎn)化為雙鏈表。如果題目要求只能使用 O(1)O(1) 內(nèi)存，則只能在遍歷的同時構(gòu)建雙鏈表，即進行指針的替換。

	我們需要用遞歸的方法來解決，假定每個遞歸調(diào)用都會返回構(gòu)建好的雙鏈表，可把問題分解為左右兩個子樹。由于左右子樹都已經(jīng)是有序的，當前結(jié)點作為中間的一個結(jié)點，把左右子樹得到的鏈表連接起來即可。

	
/*合并兩個a,b兩個循環(huán)雙向鏈表*/
Node*Append(Node*a,Node*b)
{
if(a==nullptr)returnb;
if(b==nullptr)returna;

//分別得到兩個鏈表的最后一個元素
Node*a_last=a->left;
Node*b_last=b->left;

//將兩個鏈表頭尾相連
a_last->right=b;
b->left=a_last;

a->left=b_last;
b_last->right=a;

returna;
}

/*遞歸的解決二叉樹轉(zhuǎn)換為雙鏈表*/
Node*TreeToList(Node*node)
{
if(node==nullptr)returnnullptr;

//遞歸解決子樹
Node*left_list=TreeToList(node->left);
Node*right_list=TreeToList(node->right);

//把根結(jié)點轉(zhuǎn)換為一個結(jié)點的雙鏈表，方便后面的鏈表合并
node->left=node;
node->right=node;

//合并之后即為升序排列
left_list=Append(left_list,node);
left_list=Append(left_list,right_list);

returnleft_list;
}


	

	18 有序鏈表轉(zhuǎn)化為平衡的二分查找樹（Binary Search Tree）

	我們可以采用自頂向下的方法。先找到中間結(jié)點作為根結(jié)點，然后遞歸左右兩部分。所以我們需要先找到中間結(jié)點，對于單鏈表來說，必須要遍歷一邊，可以使用快慢指針加快查找速度。

	
structTreeNode
{
intdata;
TreeNode*left;
TreeNode*right;
TreeNode(intdata_){data=data_;left=right=nullptr;}
};

structListNode
{
intdata;
ListNode*next;
ListNode(intdata_){data=data_;next=nullptr;}
};

TreeNode*SortedListToBST(ListNode*list_node)
{
if(!list_node)returnnullptr;
if(!list_node->next)return(newTreeNode(list_node->data));

//用快慢指針找到中間結(jié)點
ListNode*pre_slow=nullptr;//記錄慢指針的前一個結(jié)點
ListNode*slow=list_node;//慢指針
ListNode*fast=list_node;//快指針
while(fast&&fast->next)
{
pre_slow=slow;
slow=slow->next;
fast=fast->next->next;
}
TreeNode*mid=newTreeNode(slow->data);

//分別遞歸左右兩部分
if(pre_slow)
{
pre_slow->next=nullptr;
mid->left=SortedListToBST(list_node);
}
mid->right=SortedListToBST(slow->next);

returnmid;
}


	

	由 f(n)=2f(frac n2)+frac n2f(n)=2f(2n)+2n 得，所以上述算法的時間復雜度為 O(nlogn)O(nlogn)。

	不妨換個思路，采用自底向上的方法：

	
TreeNode*SortedListToBSTRec(ListNode*&list,intstart,intend)
{
if(start>end)returnnullptr;

intmid=start+(end-start)/2;
TreeNode*left_child=SortedListToBSTRec(list,start,mid-1);//注意此處傳入的是引用
TreeNode*parent=newTreeNode(list->data);
parent->left=left_child;
list=list->next;
parent->right=SortedListToBSTRec(list,mid+1,end);
returnparent;
}

TreeNode*SortedListToBST(ListNode*node)
{
intn=0;
ListNode*p=node;
while(p)
{
n++;
p=p->next;
}

returnSortedListToBSTRec(node,0,n-1);
}


	

	如此，時間復雜度降為 O(n)O(n)。

	19 判斷是否是二叉查找樹

	我們假定二叉樹沒有重復元素，即對于每個結(jié)點，其左右孩子都是嚴格的小于和大于。

	下面給出兩個方法：

	方法 1：

	
boolIsBST(Node*node,intmin,intmax)
{
if(node==nullptr)
returntrue;
if(node->data<=?min?||?node->data>=max)
returnfalse;

returnIsBST(node->left,min,node->data)&&IsBST(node->right,node->data,max);
}

IsBST(node,INT_MIN,INT_MAX);


	

	方法 2：

	利用二叉查找樹中序遍歷時元素遞增來判斷。

	
boolIsBST(Node*node)
{
staticintpre=INT_MIN;

if(node==nullptr)
returntrue;

if(!IsBST(node->left))
returnfalse;

if(node->datadata;

returnIsBST(node->right);
}

	

	





	審核編輯：劉清