到目前為止,我們已經(jīng)用小批量隨機(jī)梯度下降訓(xùn)練了我們的模型。然而,當(dāng)我們實(shí)現(xiàn)該算法時(shí),我們只擔(dān)心通過模型進(jìn)行前向傳播所涉及的計(jì)算。當(dāng)需要計(jì)算梯度時(shí),我們只是調(diào)用了深度學(xué)習(xí)框架提供的反向傳播函數(shù)。
梯度的自動(dòng)計(jì)算(自動(dòng)微分)大大簡(jiǎn)化了深度學(xué)習(xí)算法的實(shí)現(xiàn)。在自動(dòng)微分之前,即使是對(duì)復(fù)雜模型的微小改動(dòng)也需要手動(dòng)重新計(jì)算復(fù)雜的導(dǎo)數(shù)。令人驚訝的是,學(xué)術(shù)論文常常不得不分配大量頁面來推導(dǎo)更新規(guī)則。雖然我們必須繼續(xù)依賴自動(dòng)微分,以便我們可以專注于有趣的部分,但如果您想超越對(duì)深度學(xué)習(xí)的膚淺理解,您應(yīng)該知道這些梯度是如何在底層計(jì)算的。
在本節(jié)中,我們將深入探討反向傳播(通常稱為反向傳播)的細(xì)節(jié)。為了傳達(dá)對(duì)技術(shù)及其實(shí)現(xiàn)的一些見解,我們依賴于一些基本的數(shù)學(xué)和計(jì)算圖。首先,我們將重點(diǎn)放在具有權(quán)重衰減的單隱藏層 MLP 上(?2 正則化,將在后續(xù)章節(jié)中描述)。
5.3.1. 前向傳播
前向傳播(或forward pass)是指神經(jīng)網(wǎng)絡(luò)從輸入層到輸出層依次計(jì)算和存儲(chǔ)中間變量(包括輸出)。我們現(xiàn)在逐步了解具有一個(gè)隱藏層的神經(jīng)網(wǎng)絡(luò)的機(jī)制。這可能看起來很乏味,但用放克演奏家詹姆斯布朗的永恒名言來說,你必須“付出代價(jià)才能成為老板”。
為了簡(jiǎn)單起見,我們假設(shè)輸入示例是 x∈Rd并且我們的隱藏層不包含偏差項(xiàng)。這里的中間變量是:
(5.3.1)z=W(1)x,
在哪里W(1)∈Rh×d是隱藏層的權(quán)重參數(shù)。運(yùn)行中間變量后 z∈Rh通過激活函數(shù) ?我們獲得了長(zhǎng)度的隱藏激活向量h,
(5.3.2)h=?(z).
隱藏層輸出h也是一個(gè)中間變量。假設(shè)輸出層的參數(shù)只具有權(quán)重W(2)∈Rq×h,我們可以獲得一個(gè)輸出層變量,其向量長(zhǎng)度為q:
(5.3.3)o=W(2)h.
假設(shè)損失函數(shù)是l示例標(biāo)簽是 y,然后我們可以計(jì)算單個(gè)數(shù)據(jù)示例的損失項(xiàng),
(5.3.4)L=l(o,y).
根據(jù)定義?2我們稍后將介紹的正則化,給定超參數(shù)λ,正則化項(xiàng)是
(5.3.5)s=λ2(‖W(1)‖F(xiàn)2+‖W(2)‖F(xiàn)2),
其中矩陣的 Frobenius 范數(shù)就是?2將矩陣展平為向量后應(yīng)用范數(shù)。最后,模型在給定數(shù)據(jù)示例上的正則化損失為:
(5.3.6)J=L+s.
我們指的是J作為下面討論中的目標(biāo)函數(shù)。
5.3.2. 前向傳播的計(jì)算圖
繪制計(jì)算圖有助于我們可視化計(jì)算中運(yùn)算符和變量的依賴關(guān)系。圖 5.3.1 包含與上述簡(jiǎn)單網(wǎng)絡(luò)相關(guān)的圖形,其中方塊表示變量,圓圈表示運(yùn)算符。左下角表示輸入,右上角表示輸出。請(qǐng)注意箭頭的方向(說明數(shù)據(jù)流)主要是向右和向上。
圖 5.3.1前向傳播計(jì)算圖。
5.3.3. 反向傳播
反向傳播是指計(jì)算神經(jīng)網(wǎng)絡(luò)參數(shù)梯度的方法。簡(jiǎn)而言之,該方法根據(jù)微 積分的鏈?zhǔn)椒▌t以相反的順序遍歷網(wǎng)絡(luò),從輸出層到輸入層。該算法存儲(chǔ)計(jì)算某些參數(shù)的梯度時(shí)所需的任何中間變量(偏導(dǎo)數(shù))。假設(shè)我們有函數(shù) Y=f(X)和Z=g(Y), 其中輸入和輸出 X,Y,Z是任意形狀的張量。通過使用鏈?zhǔn)椒▌t,我們可以計(jì)算導(dǎo)數(shù) Z關(guān)于X通過
(5.3.7)?Z?X=prod(?Z?Y,?Y?X).
在這里我們使用prod運(yùn)算符在執(zhí)行必要的操作(例如轉(zhuǎn)置和交換輸入位置)后將其參數(shù)相乘。對(duì)于向量,這很簡(jiǎn)單:它只是矩陣-矩陣乘法。對(duì)于更高維的張量,我們使用適當(dāng)?shù)膶?duì)應(yīng)物。運(yùn)營(yíng)商 prod隱藏所有符號(hào)開銷。
回想一下,具有一個(gè)隱藏層的簡(jiǎn)單網(wǎng)絡(luò)的參數(shù),其計(jì)算圖如圖 5.3.1所示,是 W(1)和W(2). 反向傳播的目的是計(jì)算梯度 ?J/?W(1)和 ?J/?W(2). 為此,我們應(yīng)用鏈?zhǔn)椒▌t并依次計(jì)算每個(gè)中間變量和參數(shù)的梯度。計(jì)算的順序相對(duì)于前向傳播中執(zhí)行的順序是相反的,因?yàn)槲覀冃枰獜挠?jì)算圖的結(jié)果開始并朝著參數(shù)的方向努力。第一步是計(jì)算目標(biāo)函數(shù)的梯度J=L+s關(guān)于損失期限 L和正則化項(xiàng)s.
(5.3.8)?J?L=1and?J?s=1.
接下來,我們計(jì)算目標(biāo)函數(shù)相對(duì)于輸出層變量的梯度o根據(jù)鏈?zhǔn)椒▌t:
(5.3.9)?J?o=prod(?J?L,?L?o)=?L?o∈Rq.
接下來,我們計(jì)算關(guān)于兩個(gè)參數(shù)的正則化項(xiàng)的梯度:
(5.3.10)?s?W(1)=λW(1)and?s?W(2)=λW(2).
現(xiàn)在我們可以計(jì)算梯度了 ?J/?W(2)∈Rq×h 最接近輸出層的模型參數(shù)。使用鏈?zhǔn)揭?guī)則產(chǎn)生:
(5.3.11)?J?W(2)=prod(?J?o,?o?W(2))+prod(?J?s,?s?W(2))=?J?oh?+λW(2).
獲得關(guān)于的梯度W(1)我們需要繼續(xù)沿著輸出層反向傳播到隱藏層。關(guān)于隱藏層輸出的梯度 ?J/?h∈Rh是(誰)給的
(5.3.12)?J?h=prod(?J?o,?o?h)=W(2)??J?o.
由于激活函數(shù)?按元素應(yīng)用,計(jì)算梯度 ?J/?z∈Rh中間變量的z要求我們使用逐元素乘法運(yùn)算符,我們用⊙:
(5.3.13)?J?z=prod(?J?h,?h?z)=?J?h⊙?′(z).
最后,我們可以得到梯度 ?J/?W(1)∈Rh×d 最接近輸入層的模型參數(shù)。根據(jù)鏈?zhǔn)椒▌t,我們得到
(5.3.14)?J?W(1)=prod(?J?z,?z?W(1))+prod(?J?s,?s?W(1))=?J?zx?+λW(1).
5.3.4. 訓(xùn)練神經(jīng)網(wǎng)絡(luò)
在訓(xùn)練神經(jīng)網(wǎng)絡(luò)時(shí),前向傳播和反向傳播相互依賴。特別是,對(duì)于前向傳播,我們沿依賴方向遍歷計(jì)算圖并計(jì)算其路徑上的所有變量。然后將這些用于反向傳播,其中圖上的計(jì)算順序是相反的。
以前述簡(jiǎn)單網(wǎng)絡(luò)為例進(jìn)行說明。一方面,在前向傳播過程中計(jì)算正則化項(xiàng)(5.3.5) 取決于模型參數(shù)的當(dāng)前值W(1)和W(2). 它們由優(yōu)化算法根據(jù)最近一次迭代中的反向傳播給出。另一方面,反向傳播過程中參數(shù)(5.3.11)的梯度計(jì)算取決于隱藏層輸出的當(dāng)前值h,這是由前向傳播給出的。
因此在訓(xùn)練神經(jīng)網(wǎng)絡(luò)時(shí),在初始化模型參數(shù)后,我們交替進(jìn)行正向傳播和反向傳播,使用反向傳播給出的梯度更新模型參數(shù)。請(qǐng)注意,反向傳播會(huì)重用前向傳播中存儲(chǔ)的中間值以避免重復(fù)計(jì)算。結(jié)果之一是我們需要保留中間值,直到反向傳播完成。這也是為什么訓(xùn)練比普通預(yù)測(cè)需要更多內(nèi)存的原因之一。此外,這些中間值的大小大致與網(wǎng)絡(luò)層數(shù)和批量大小成正比。因此,使用更大的批量大小訓(xùn)練更深的網(wǎng)絡(luò)更容易導(dǎo)致內(nèi)存不足錯(cuò)誤。
5.3.5. 概括
前向傳播在神經(jīng)網(wǎng)絡(luò)定義的計(jì)算圖中順序計(jì)算和存儲(chǔ)中間變量。它從輸入層進(jìn)行到輸出層。反向傳播以相反的順序順序計(jì)算并存儲(chǔ)神經(jīng)網(wǎng)絡(luò)中中間變量和參數(shù)的梯度。在訓(xùn)練深度學(xué)習(xí)模型時(shí),正向傳播和反向傳播是相互依賴的,訓(xùn)練需要的內(nèi)存明顯多于預(yù)測(cè)。
5.3.6. 練習(xí)
假設(shè)輸入X一些標(biāo)量函數(shù) f是n×m矩陣。梯度的維數(shù)是多少f關(guān)于X?
向本節(jié)中描述的模型的隱藏層添加偏差(您不需要在正則化項(xiàng)中包含偏差)。
畫出相應(yīng)的計(jì)算圖。
推導(dǎo)前向和反向傳播方程。
計(jì)算本節(jié)中描述的模型中訓(xùn)練和預(yù)測(cè)的內(nèi)存占用量。
假設(shè)您要計(jì)算二階導(dǎo)數(shù)。計(jì)算圖會(huì)發(fā)生什么變化?您預(yù)計(jì)計(jì)算需要多長(zhǎng)時(shí)間?
假設(shè)計(jì)算圖對(duì)于您的 GPU 來說太大了。
您可以將它分區(qū)到多個(gè) GPU 上嗎?
與在較小的 minibatch 上進(jìn)行訓(xùn)練相比,優(yōu)缺點(diǎn)是什么?
審核編輯黃宇
Discussions
-
pytorch
+關(guān)注
關(guān)注
2文章
809瀏覽量
13881
發(fā)布評(píng)論請(qǐng)先 登錄
解讀多層神經(jīng)網(wǎng)絡(luò)反向傳播原理
手動(dòng)設(shè)計(jì)一個(gè)卷積神經(jīng)網(wǎng)絡(luò)(前向傳播和反向傳播)
人工智能(AI)學(xué)習(xí):如何講解BP(反向傳播)流程

淺析深度神經(jīng)網(wǎng)絡(luò)(DNN)反向傳播算法(BP)
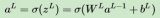
PyTorch教程5.3之前向傳播、反向傳播和計(jì)算圖

PyTorch教程之時(shí)間反向傳播

PyTorch教程-9.7. 時(shí)間反向傳播
神經(jīng)網(wǎng)絡(luò)前向傳播和反向傳播區(qū)別
神經(jīng)網(wǎng)絡(luò)前向傳播和反向傳播在神經(jīng)網(wǎng)絡(luò)訓(xùn)練過程中的作用
神經(jīng)網(wǎng)絡(luò)反向傳播算法的推導(dǎo)過程
神經(jīng)網(wǎng)絡(luò)反向傳播算法的優(yōu)缺點(diǎn)有哪些
【每天學(xué)點(diǎn)AI】前向傳播、損失函數(shù)、反向傳播






 PyTorch教程-5.3. 前向傳播、反向傳播和計(jì)算圖
PyTorch教程-5.3. 前向傳播、反向傳播和計(jì)算圖











評(píng)論